AB测试听起来原理很简单，控制变量法看看用户对于一个策略的实施是否有明显效果。

但是在当今互联网大规模地构建一个正确可靠的A/B测试平台仍然是一个巨大的挑战：不仅要在实验设计环节应对溢出效应和小样本的双重挑战，平衡好实验偏差与方差以确定合适的实验单元、分组方法和分析方法，给出合理的实验设计，而且要在分析环节应对方差计算、P值计算、多重比较、混淆因素、假阴性（实际策略有效果，但是检测显示无效果）等多种统计陷阱。

因此，要获得高质量的结果需要对实验和统计有专家级的理解，这无疑增加了实验门槛，难以达成任何人进行实验都可得出可信结论的目标。本文会从统计、工程角度详细介绍当代互联网AB测试工程的场景特点及最前沿解决方案。

本文主要站在互联网数据科学家角度，尽量做到沉淀经验和统计细节兼备。致力于涵盖所有AB测试相关模块，三万字读懂工业界AB测试的应用。

目录

• 一.AB测试及其统计原理
  • 1.1 假设检验
  • 1.2 AB结果有意义需要满足的三个基本要素
• 二.业界AB测试的一般步骤
  • 2.1 分流
    • 2.1.1 基于层、域嵌套的重叠分流框架
    • 2.1.2 基于冲突检测的分流框架
  • 2.2 实验设计
    • 2.2.1 明确改动点
    • 2.2.2 指标类型与加工逻辑
      • 2.2.2.1 指标业务类型
      • 2.2.2.2 指标统计类型
    • 2.2.3 实验分组方式
    • 2.2.4 分流单元
    • 2.2.5 样本量预估
      • 2.2.5.1 样本量预估公式
      • 2.2.5.2 生产场景中的确认指标
        • 2.2.5.2.1 AB测试的本质:H0到底正不正确？
        • 2.2.5.2.2 Baseline rate
        • 2.2.5.2.3 Minimum Detectable Effect
    • 2.2.6 增加p值显著速度
      • 2.2.6.1 降方差（Variance Reduction）
        • 2.2.6.1.1 CUPED降方差
        • 2.2.6.1.2 Stratified Sampling
        • 2.2.6.1.3 Post Stratification
  • 2.3 统计引擎
    • 2.3.1 数据诊断
    • 2.3.2 选择效应估计方法
      • 2.3.2.1 差值法
      • 2.3.2.2 DID双重差分
        • 2.3.2.2.1 DID双重差分介绍
        • 2.3.2.2.1 DID双重差分需要满足的假设
        • 2.3.2.2.1.1 线性关系假设
        • 2.3.2.2.1.2 个体处理稳定性假设
        • 2.3.2.2.1.3 平行趋势假设
        • 2.3.2.2.1.3.1 对模型处理：
        • 2.3.2.2.1.3.1.1 经典DID模型
        • 2.3.2.2.1.3.1.2 异时DID
        • 2.3.2.2.1.3.1.3 广义DID
        • 2.3.2.2.1.3.1.4.异质性DID
        • 2.3.2.2.1.3.1.5 三重差分法
        • 2.3.2.2.1.3.2 对数据处理
        • 2.3.2.2.1.3.2.1 倾向得分匹配
        • 2.3.2.2.1.3.2.2 合成控制法
    • 2.3.4 方差计算
      • 2.3.4.1 方差错误导致统计陷阱
      • 2.3.4.2 正确计算方差的方法
    • 2.3.5 p_value显著性检验
      • 2.3.5.1 p_value检验陷阱
      • 2.3.5.2 p_value检验方式
• 三.AB测试的一般人员分工
• 四.AA测试
• 五.生产上多种多样的AB测试
  • 5.1 随机轮转实验
  • 5.2 更高效的AB测试–interleaving
  • 5.3 用户裂变场景怎么避免污染
  • 5.4 低响应场景

一.AB测试及其统计原理

在这一章我会根据工程实践中的AB实践流程及理论基础进行详细介绍。

AB测试，又叫随机对照试验，来源于假设检验，我们现在有两个随机均匀的样本组A、B，对其中一个组A做出某种改动，实验结束后分析两组用户行为数据，通过显著性检验，判断这个改动对于我们所关注的核心指标是否有显著的影响。

如果我们在做完实验之后，通过显著性检验发现P值足够小，我们则推翻原假设，证明这项改动会对我们所关注的核心指标产生显著影响，否则接受原假设，认为该改动未产生显著影响。如果用一句话来概括的话，AB测试其实就是随机均匀样本组的对照实验。这个就是AB测试的原理。

1.1 假设检验

先想一个例子，我们做了一次AB测试，获得实验组A组转化率8%，和对照组B组转化率7%，此时8%>7%，但是我们能直接说A组有效果吗？不能，因为有可能是因为正常的波动导致的，无统计学意义（不显著）。

那该怎么证明其有统计学意义呢？答案是假设检验，假设检验基于一个非常朴素的想法：如果一件事发生的概率小于$\alpha$(一般取0.05)，那么它就不会发生。如果发生了，那肯定是前提假设有问题。所以假设检验实际上是一个先做原假设，再推翻的过程。

故A/B测试的假设检验包含两个假设：

原假设（Null hypothesis, 也叫$H0$）：我们希望通过实验结果推翻的假设。在上述例子里，原假设可以表述为“A和B无明显区别，即A的算法无提升”。

备择假设（Alternative hypothesis, 也叫$H1$）：我们希望通过实验结果验证的假设。在上述例子里，可以表述为“A与B有明显区别，即A的算法有明显提升（单侧）”。

我们要计算的概率则是在“A和B无明显区别，即A的算法无提升”的假设下，A组呈现8%转化率的概率。统计学中我们想计算一个事件的概率首先需要知道其分布。幸运的是我们随机抽样的行为符合中心极限定理：即对于独立并同样分布的随机变量，即使原始变量本身不是正态分布，标准化样本均值的抽样分布也趋向于标准正态分布，用人话说就是无论原始变量如何分布，对其进行n次抽样，每次抽样抽取m个样本，只要n和m足够大，这n次抽样出的n个样本均值就趋向于正态分布，且均值与原始变量均值趋于相同。

回到上述例子，B组的转化率为7%，基于原假设（A组与B组无明显差异），我们认为A组应该符合一个均值为7%的正态分布。为了方便计算，将其规则化为为均值为0的、方差为1的标准正态分布，计算规则化后的数值标准正态分布进行比较，如果落在下图空白部分，即大于1.65或小于-1.65，那么认为此事件发生概率小于5%。

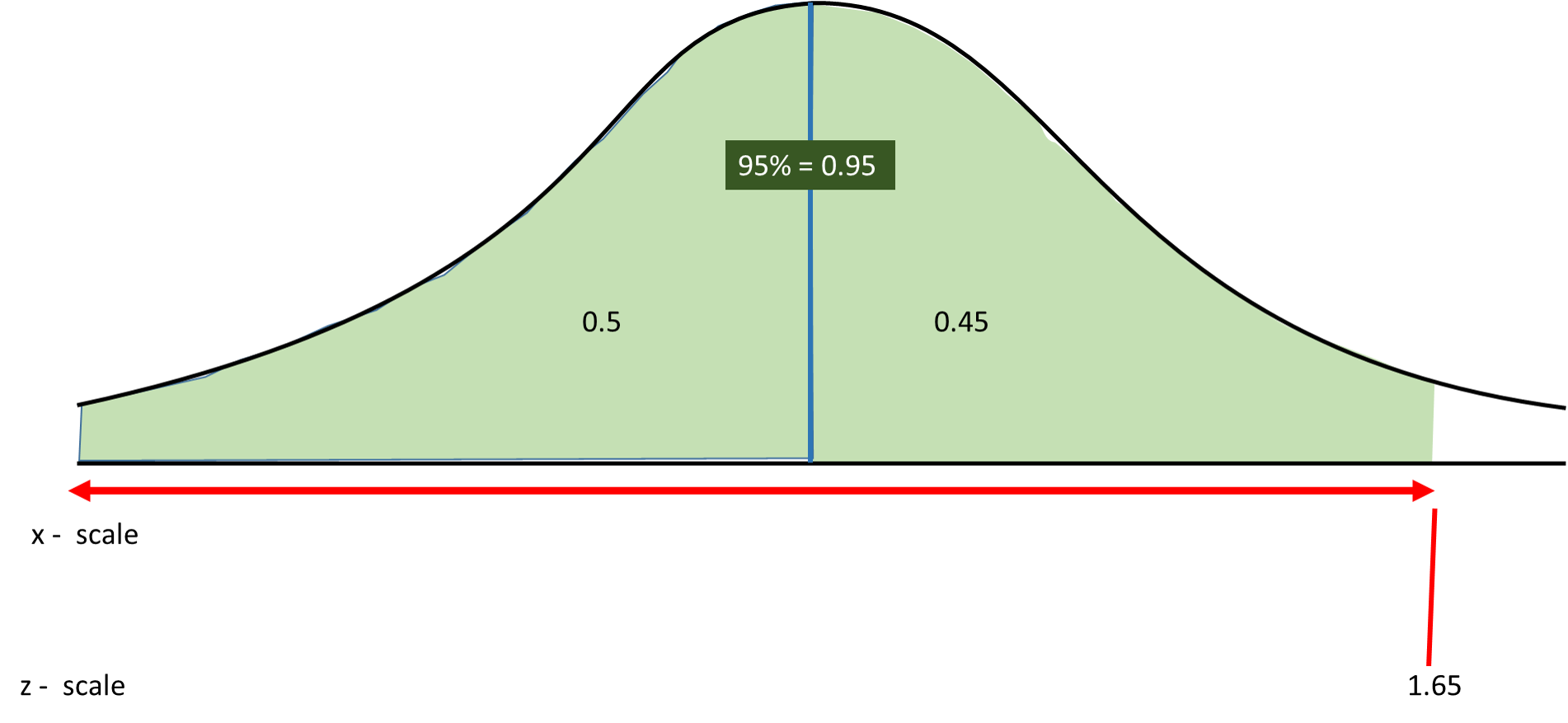
如果概率概率小于5%的事件让我一次就观测到了，这不符合常理，那么原假设并不正确，我们得到了有统计学意义的结果：A组的策略确实让转化率得到了提升，可以持续应用于实践。

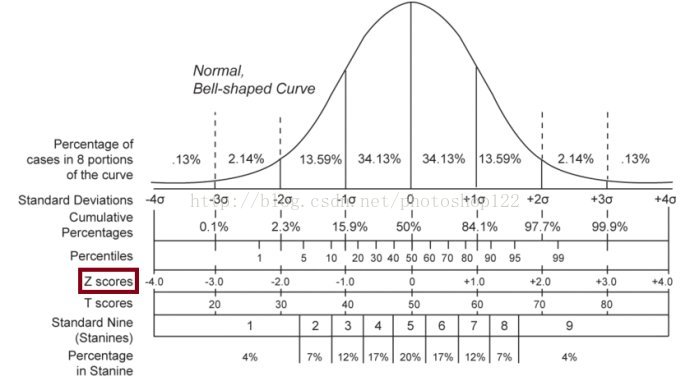
继续深入，上面提到的“将其规则化为为均值为0的、方差为1的标准正态分布”的规则化方法具体公式是什么呢。

在统计学中，有明确的公式如下。

• 绝对值类指标。我们平常直接计算就能得到的单个指标，不需要多个指标计算得到。一般都是统计该指标在一段时间内的均值或者汇总值，比如DAU，平均停留时长等。这类指标一般较少作为AB测试的观测指标。

对于绝对值指标，我们使用t检验判断AB两组的表现是否有均值差异：

$$t=\cfrac{(\bar x - \mu _0)}{\sqrt{s/n}}$$

其中$\bar x$为抽样的样本均值，$\mu _0$为要推翻的均值（AB测试中为B组的均值）,S为抽样的标准差，n为抽样的样本量。

• 比率类指标。与绝对值类指标相对应，我们不能直接计算得到，而是通过多个指标计算得到。比如某页面的点击率，我们需要先计算页面的点击数和展现数，两者相除才能得到该指标。类似的，还有一些转化率、复购率等等。AB测试观测的大部分指标都是比率类指标。

对于比率类指标，我们使用基于伯努利概率的Z检验判断AB两组的表现是否有比率差异：

$$Z=\cfrac{\bar p - p_0}{\sqrt{p_0(1-p_0)/n}}$$

其中$\bar p$为抽样样本的比例，$p_0$为要推翻的比例，n为抽样的样本量。

为了直观理解上述公式，回到刚才的例子跟我想象三个情况：

• 如果A组转化率为20%呢？是不是我们认为20%比B组的7%大很多所以更有可能是策略导致而非正常波动。
• 如果我告诉你，正常情况下B组的转化率方差很小，一般都只在3.8%-4.2%之间波动呢？是不是我们就认为此时策略实施后提升到5%，更有可能是策略生效，而非正常波动。
• 如果A组和B组的样本量有分别有100个用户，10000个用户和100万个用户，哪个看起来更能证明策略生效呢？当然是100万个用户，因为样本量的提升会自然抵抗异常值导致的波动。

到这里，我们应该就理解A组对比B组是否显著有效，不仅与A组($p_1$)本身相对B组($p_0$)的提升有关，还与AB组的方差($\sigma$)、样本量(n)有关。且A组相对B组提升越大、方差越小、样本量越大，统计结果越显著。后续我们的实验策略和结果分析都会围绕这几点来进行。

1.2 AB结果有意义需要满足的三个基本要素

基于假设检验的原理，我们发现在运行AB实验时，要满足三个基本要素：

①施加不同策略的实验组、对照组可比较，即实验组、对照组的特征均值在实验前相同或在实验前具有固定差异，便于实验后计算哪些差异是由于策略不同导致的；

• 否则，实验后难以确定实验组对照组的差异是由策略导致的还是由于分组导致的，难以准确衡量策略的真实效应；

②策略之间没有干扰，实验群体相互独立，即当我们比较策略A和策略B时，接受策略A的用户行为不会受接受策略B的用户行为影响；

• 否则，可能会高估策略效应。举个例子，在履约配送范围实验中，橘色是实验组，商户A范围的扩大，会使用户的需求从商户B转移到商户A，如果评估的是商户集合的单量，会造成实验组单量相对对照组多，实验环节，得出扩大配送范围，会提高整体单量，但是当策略在全国应用后，发现单量并没有明显增加，因为实验期间观察的增加仅仅是单量转移，实验组单量转移到了对照组。

③实验群体的数量要足够，以满足功效要求，避免实验结果假阴性，即实际策略有效果但是由于样本量不足没有检测出来。

• 否则，难以确定策略无效果是真正的无效果还是由于样本量不足，没有检测到策略效果。

二.业界AB测试的一般步骤

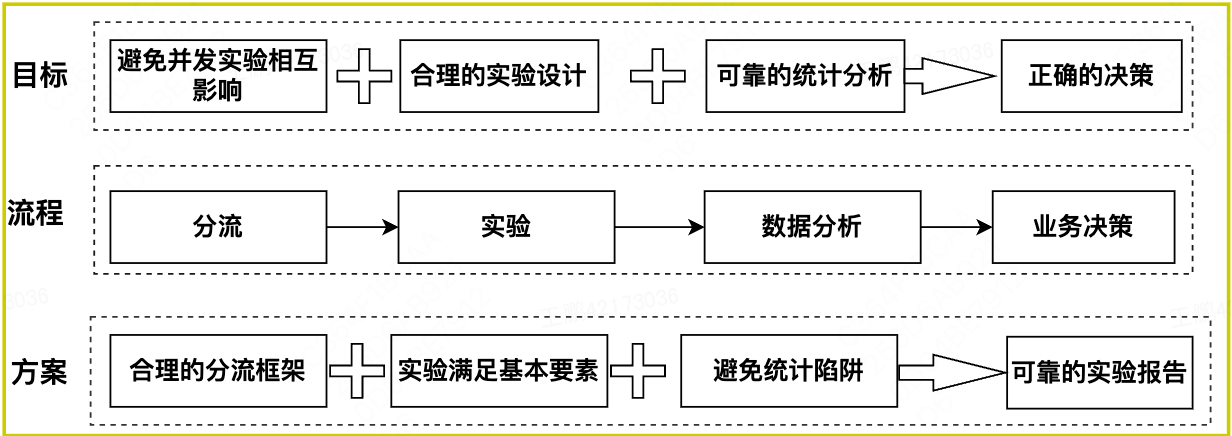
不管何种类型的AB实验，都符合分流->实验->数据分析->决策的基本流程，以及需要满足AB实验的3个基本要素。分流是实验平台的顶层设计，它规范和约束了不同实验者如何在平台上独立运行各自实验而不相互影响，运行实验，看似简单，但是成功运行不同类型实验的前提是实验场景要满足其理论假设。

AB实验主要是通过观察抽样的样本来推断总体的行为，属于预测型结论，数据分析涉及大量的统计学理论，稍有不慎，容易掉入统计陷阱。上述流程，任一环节出错，都可能导致错误的结论，因此，AB实验统计一个数字容易，得到可靠可信的统计结论并不容易。

2.1 分流

通过实验衡量真实的用户反应，以确定新产品功能的效果，如果无法同时运行多个并行实验，将会大大减慢迭代速度。扩大同时运行实验的数量对于实现更快的迭代是必不可少的。

分流框架像法律法规规范着规范着大家的日常行为，使大家在社会大家庭中有序生活一样，它规范和约束着不同的实验在不相互影响的前提下如何共享和使用流量，它是实验平台的顶层设计。基于约束的分流框架让实验者指定约束，平台冲突检测根据实验者指定的约束，进一步判断是否允许实验。

为了增加可以同时运行的实验数量，提高并行性，并允许同时运行多个互斥实验，业界出现了两种分流框架，一种是像谷歌、微软、脸书这种单边业务形态的公司，采用层、域嵌套的分流框架；另一种是像Uber、DoorDash这种多边业务形态的公司，采用基于约束的分流框架。具体如下图所示：

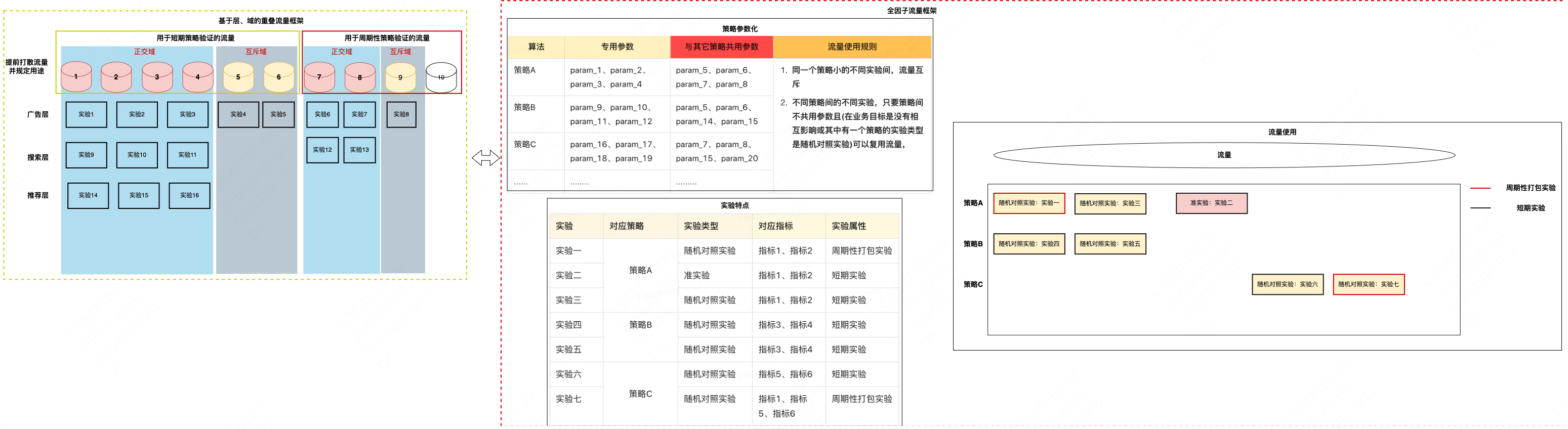
2.1.1 基于层、域嵌套的重叠分流框架

该分流框架的特点是事先将流量随机打散做桶号标识并提前规划流量的用途，如上图所示，提前将全国流量划分为10等份并用1到10桶号来标识流量，1-6号桶的流量用于短期策略验证，7-10号桶用于长期性策略验证。为了支持同时运行多个互斥实验，提升迭代效率，分别在1-6号桶和7-10号桶中，进一步区分了正交桶和互斥桶，落在正交桶中的流量可以同时进入多个实验，在每进入一个实验前，重新打散一次流量，避免上一实验的残留效应做下一实验造成影响，实现了多个互斥实验的并行运行，落在互斥桶的流量，每次只能进入一个实验，用于运行不满足随机打散条件的实验。基于桶号划分的用于特定用途的一组流量集合，我们称为域；同一流量进入的不同类型的实验，我们称为层。

该分流框架的优点是不仅可以实现流量复用，扩大实验并行度，而且较容易避免具有潜在交互作用的实验可能给用户带来的糟糕体验。引入层的概念，将系统参数划分为多个层，约束让组合在一起可能产生较差用户体验的实验必须位于同一层，同一用户可进入不同层多个实验以实验流量复用，并防止其进入同一层多个实验，避免糟糕的用户体验。

不足之处在于：首先，这种分流框架的一大前提是提前将流量打散，这种在大流量的单边场景下尚可，在小流量的多边场景下，难以行得通。多边场景下，考虑到溢出效应，无法直接采用单边实体进行分流，而是采用聚类的方式将有相互作用的多边聚合成一个大的实体，基于大的实体进行分流，考虑到有限的实体数量，这种提前打散的方式难以获得均匀的流量；其次，域提前规定了流量用途，这种提前隔离的方式，降低了流量利用率，无法满足小流量场下实验功效要求，如即使在互斥域中没有实验，也无法采用该流量进行其它的正交实验；第三，这种提前预规划流量用途的分流框架灵活性不足，如果后期发现域的设置不合理，要改变域的配置将付出较大的代价。

2.1.2 基于冲突检测的分流框架

该分流框架的特点是由实验者制定约束，平台根据实验者制定的约束，确保无法避免潜在交互影响的实验没有同时曝光给用户。如微软、Uber等公司，实验平台都集成了检测交互作用的自动化系统，以避免实验间潜在交互影响。以Uber为例，将策略看作是一组独立参数的集合，并提前声明对应策略涉及的专用参数和与其它策略共享的参数，配置实验时检测是否有任何影响相同参数的两个实验重叠，只要它们没有重叠，便允许实验创建或更新操作。

该分流框架的优点是灵活且能最大限度的复用流量，相较于重叠流量框架，不受提前划分的域的约束只能在特定域中进行实验，即使对应的域中此时并无其它实验。只要满足进行并行实验的条件，便可以任意圈定流量进行实验；不足之处在于：实验平台需要构建自动检测交互作用的能力。

以美团的基于冲突检测的分流框架为例，介绍约束框架的设计思路。

在展开之前，先引入三个概念：算法Key、场景和实验模版。

算法Key代表一组可独立测试的功能，在技术层面可以表示为一组独立参数集合，场景代表对应算法Key（对于联合实验而言，是多个算法Key；非联合实验，是一个算法Key）下具有相同实验模版的实验集合，实验模版为一组相同实验类型、实验单位、分组方法、评估方法的配置。

考虑到：

①同一算法Key，不同实验是针对同一功能不同版本的测试，实验间要互斥；

②不同算法Key之间，只要其对应的功能之间没有潜在的交互作用，其对应的实验间天然正交可以放心的复用流量，如存在潜在交互作用，只要确保流量能被随机打散，便可消除策略间的潜在相互作用对实验结论的影响。

因此，针对并行实验，初步的约束如下：

①同一算法Key下的任意两个实验不能复用流量，冲突；

②不同算法Key下存在潜在交互作用的两个实验，只要有一个实验类型是随机对照实验，皆可复用流量。约束②不仅避免了全因子流量框架不同策略实验间潜在相互影响的风险，而且避免了重叠流量框架因不同域流量隔离导致的流量复用率低的问题，特别是在准实验、观察性研究比随机对照实验多的情形下，由于准实验、观察性研究分处不同的域，无法实现随机对照实验和准实验、观察性研究之间的流量复用。

考虑到同一算法Key下不同实验因目标流量或迭代验证的功能不同，同一个算法Key下的不同实验与另一算法Key下的不同实验间是否冲突取决于其对应的测试功能或实验方法，我们引入场景来描述不同算法Key的功能描述和其对应的实验方法，并根据业务经验构造不同场景间的业务影响矩阵。基于不同场景的业务影响矩阵、场景实验方法和并行实验约束，生成场景实验冲突矩阵，基于此矩阵完成不同算法Key实验间的冲突检测。

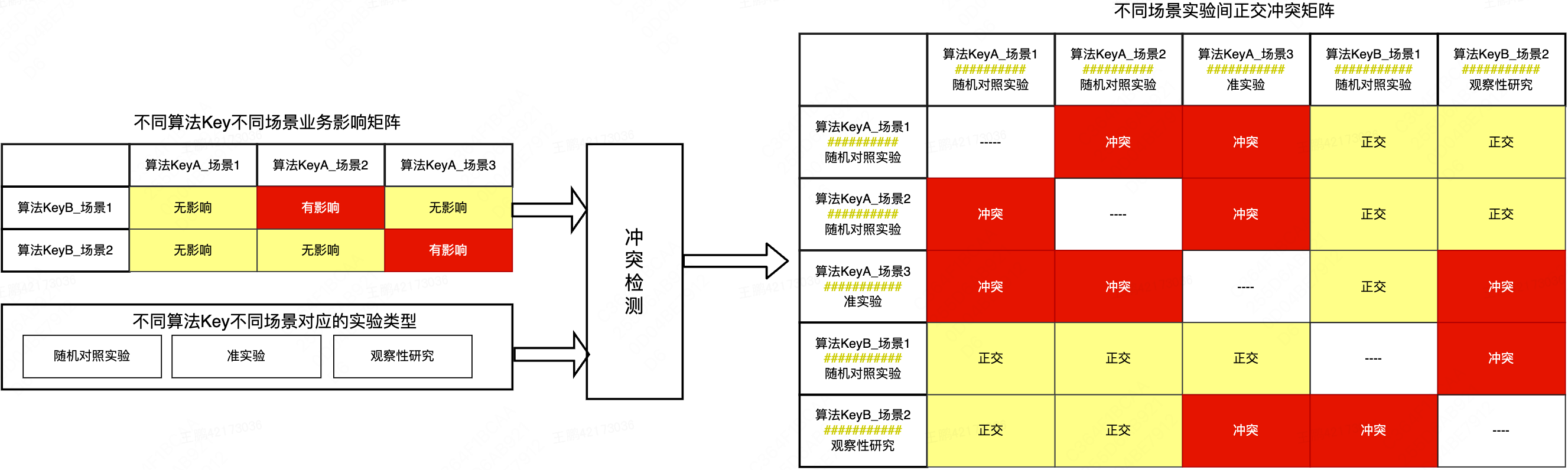
不同场景下的联合实验，与其对应算法Key下所有场景实验冲突，与其它算法Key场景实验，根据约束2进一步判定；为避免冲突实验间的流量重叠，提供了基于表达式定义流量范围的能力，通过检测表达式流量覆盖范围避免冲突实验间的流量重叠。基于约束的分流框架，不预先规划流量用途，也没有层、域复杂概念，实验时按需选择流量，只要通过冲突检测，就可以上线实验，不仅降低了用户使用门槛，而且提高了平台灵活性，以适应履约业务场景。

2.2 实验设计

实验设计是降低溢出效应、提高实验功效、关注实验公平等多种目标进行方差和偏差平衡的过程。

2.2.1 明确改动点

这是AB测试最为重要的一点，只有我们知道我们要验证什么，我们的AB测试才能真正发挥作用。否则做了很多工作后，发现重要指标我们甚至没有埋点监控，这就浪费了我们的工作时间。

故实验开始之前，首先要和产品或者项目经理明确实验的变量是什么？我们要保证AB测试的“单一因素原则”，即每一个实验的评估的因素都是单一因素，一次实验不能糅合多个影响因素，否则会导致实验效果难以区分是哪个因素的影响。

2.2.2 指标类型与加工逻辑

2.2.2.1 指标业务类型

• 核心指标 核心数据指标通常情况下只有一个，或者是极少数指标的合集，很多时候是一家公司或组织的核心 KPI，可以驱动业务核心价值，比如注册转化率（衡量注册流程优化试验效果）、活动按钮点击率（评估某项推广活动试验的 CTR 效果）、人均使用时长（评估某项推荐算法对用户粘性的改进效果）等。 在确定核心指标时，需要满足两个关键原则：第一，简单的，易理解的，可以在公司/团队范围内被广泛接受；第二，相对稳定的，无需频繁为了一个新功能更新核心指标。 核心指标除了用来衡量试验的效果，还可以用来计算试验所需的样本量（将在后文中详细介绍），由此可见，核心指标直接关系着试验的成败，需要重点关注。

• 驱动指标 驱动指标一般比核心指标更短期，变化更快也更灵敏，帮助我们更加快速、全面地观测业务变化。我们可以通过两个案例做进一步了解： 在某项商品推广活动试验中，核心指标是下单转化率，运营同学可以使用客单价、人均下单次数、退货率等作为驱动指标。观察发现，虽然下单率有所提升，但退货率或客单价指标下降，此时便需要做针对性调整。 某个视频推荐列表试验中，核心指标是人均播放视频数量，驱动指标是完播率、人均观看时长，通过核心指标和多个驱动指标的配合来进行推荐算法效果的评估。 通过以上我们可以看出，驱动指标能够帮助我们从更多、更全面的角度来观察试验给业务带来的影响，尤其是当发现问题时，能够帮助我们及时分析原因、调整策略，通过不断优化达到最终的试验目的。 在确定驱动指标时，需要满足三个原则：第一，驱动指标与核心指标的目标一致，能够直接反映业务变化；第二，当指标发生变化时，能够有既定的途径和方法来优化指标，是可行动、与业务相关的；第三，驱动指标是核心指标的先导指数，需要具备足够的灵敏性，快速衡量大部分试验的效果。

• 护栏指标 护栏指标，可以理解为保护业务的指标，在实际应用过程中，护栏指标的异常可以有效反映出试验设计、基础设施、数据处理环节是否正常，能够帮助我们在评价试验效果时做出正确的权衡取舍，避免因为短期指标优化影响长期指标，从而得出值得信任的试验结果。 举个例子，我们在试验中设置一定的比例让用户命中试验分组（通常建议各组流量平均分配），实际运行中如果发现样本量和构建时的预期不一致，那么可以猜测是否是分流服务出了问题，导致可信度降低。

2.2.2.2 指标统计类型

对于绝对值类指标和比率类指标，我们的P值计算公式不同，后续在统计引擎部分会进行详细介绍。

• 绝对值类指标。我们平常直接计算就能得到的单个指标，不需要多个指标计算得到。一般都是统计该指标在一段时间内的均值或者汇总值，比如DAU，平均停留时长等。这类指标一般较少作为AB测试的观测指标。

• 比率类指标。与绝对值类指标相对应，我们不能直接计算得到，而是通过多个指标计算得到。比如某页面的点击率，我们需要先计算页面的点击数和展现数，两者相除才能得到该指标。类似的，还有一些转化率、复购率等等。AB测试观测的大部分指标都是比率类指标。

2.2.3 实验分组方式

根据能否在实验前控制策略的分配，我们将实验分为AB实验和观察性研究（Observational Studies），在AB实验分支下，根据能否控制策略的随机分配，又将AB实验分为随机对照实验（Randomized Experiments）和准实验（Quasi Experiments）。

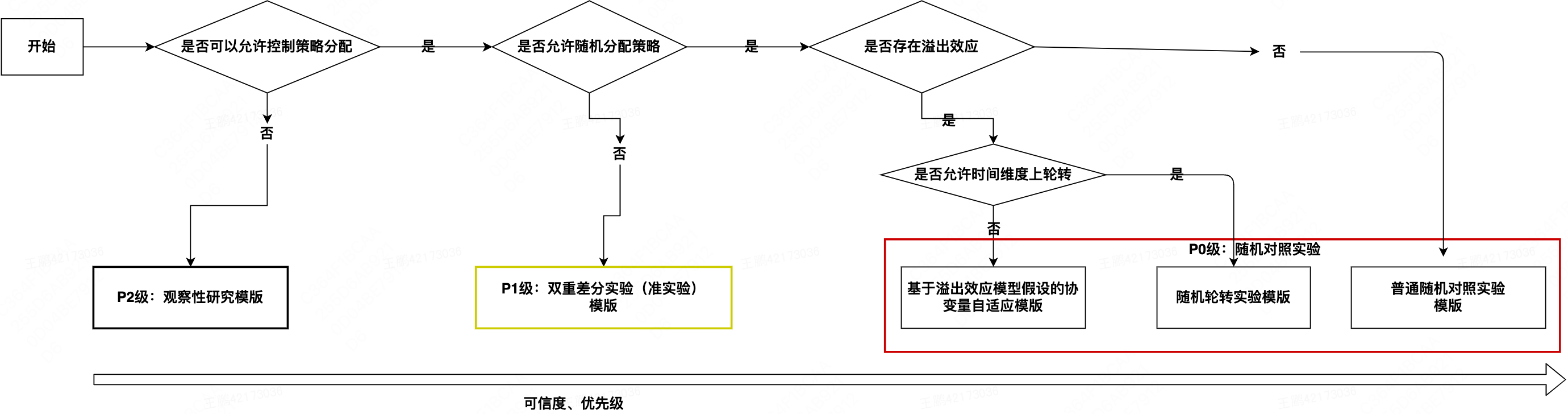
• 随机对照实验 可以控制对实验对象施加策略的场景，如①测试不同的产品UI对用户的影响，进而决定使用哪种UI；②快速验证首页商品列表图素材对转化率的影响。这些典型的C端实验场景，不仅有海量用户且用户在实验组、对照组间的行为不会相互影响，可以通过随机分组的方式找到同质且独立的实验组和对照组，这类实验称之为随机对照实验，是业界衡量策略效应的黄金标准。

• 准实验 我们不能对实验对象进行随机分配，只能有选择的进行实验组和对照组的分配，这种虽然能够控制策略分配但不能控制策略随机分配的实验，我们称之为准实验，常用的准实验方法如双重差分。

随机对照实验，因为其能够保证实验组、对照组两组的特征均值相同，不会因为分组差异干扰对真实效应的衡量，是业界衡量策略效应的黄金标准。在不满足随机对照实验约束的业务场景下衡量策略效应，我们采用准实验的方法，通过改进分组方法消除实验组、对照组可观测特征的差异或使其保持恒定差异，分析环节采用适配准实验场景的分析方法。

如果由于场景约束，只能基于实验后得到的数据来进行实验的话，就只能采用适用于观察性研究的方法。准实验和观察性研究虽然不是衡量策略效应的金标准，但是如果使用得当，也可以得出相对科学可信的分析结论。

2.2.4 分流单元

分流单元，顾名思义是接受实验的最小粒度单元，在典型的C端实验场景中，例如：测试不同的产品UI对用户的影响，进而决定使用哪种UI。此时测试的最小分流单元为单个用户。但在一些特殊场景中无法根据单个用户划分，这些场景可能需要基于地理区域划分。 此时实验方式下应该采用多大的分流单元，是综合考虑溢出效应、实验功效、公平性等因素多方平衡的结果。 例如，在美团的履约场景实验中，实验组、对照组运单可以来源于同一区域，由于同一区域的运单可以共享骑手，运单间不独立，导致实验组、对照组存在溢出效应。轮转实验是解决该问题的一个可选项，前提是我们需要在如下两个相互冲突的目标之间做平衡。

• 我们希望可以划分更多的实验单元来增加样本量，这就需要我们将实验单元划的足够小以得出更多的实验单元来保障我们有更多的样本量来满足实验灵敏度要求。
• 我们希望实验单元划的足够大确保将相互影响的个体包含在一个独立单元中，以消除溢出效应对实验结果的影响。

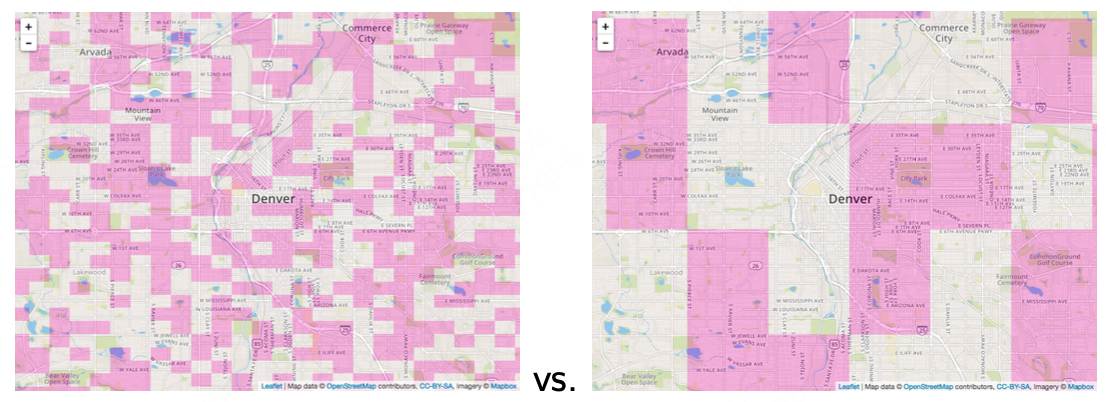
在有限的样本下，如果只是进行简单的随机分组，不仅会导致实验组对照组的一些指标在实验前存在偏差，而且会由于样本量不足导致无法检测出策略的微小提升，我们到底是通过控制影响指标差异的协变量和改进分组方式来达成偏差和方差的平衡，还是实验前允许偏差存在，通过实验后纠偏的方法进行补充，这些都需要在实验设计时基于算力，以及基于分组方式和分析方法组合方案得出的数据表现综合判断，来制定合理的实验方案。

2.2.5 样本量预估

2.2.5.1 样本量预估公式

回顾1.1章假设检验，无论是还是比率型指标，p值都与且只与，A组值，B组值，方差及样本量有关。

将样本量表达式提出：

$$n=\cfrac{\sigma^2}{\Delta^2}(Z_{\alpha/2}+Z_\beta)^2$$

其中$n$是每组所需样本量，因为A/B测试一般至少2组，所以实验所需样本量为2n； α和β分别称为第一类错误概率和第二类错误概率，一般分别取0.05和0.2； Z为正态分布的分位数函数； Δ为两组数值的差异，如点击率1%到1.5%，那么Δ就是0.5%； σ为标准差，是数值波动性的衡量，σ越大表示数值波动越厉害。

当观测的指标为绝对值类型/比率型指标时，σ的计算公式有所差异。

观测指标可以分为两种类型：

1、绝对值类指标。

$$\sigma^2=\cfrac{2*\sum^n_1(x_i-\bar x)^2}{n-1}$$

2、比率类指标。

$$\sigma^2=p_1·(1-p_1)+p_2·(1-p_2)$$

上面式子中$p_1$我们称为基础值，是实验关注的关键指标现在的数值（对照组）；$p_2$我们称为目标值，是希望通过实验将其改善至的水平；第一类错误和第二类错误上边已经提到，暂不多做说明，通常设定α为0.05，β为0.2。

从上述两个公式可以知道，在其他条件不变的情况下，如果数据本身的波动性较小，或实验两组数值差异越大，所需要的样本量就越小。从直观上看，就是本身越平稳时产生的较大变化越明显，那么需要的样本量证明越小。

2.2.5.2 生产场景中的确认指标

由于在AB测试中，比率型指标更常用，我们以比率型指标为例，比例类数值的假设检验在统计学中叫做两样本比例假设检验。在实际生产场景中，要确定这个最小样本量，我们只需要确认这四个指标：

$1-β$：Statistical power

α：Significance level

$p_1$：Baseline rate

$p_2-p_1$：Minimum detectable effect

2.2.5.2.1 AB测试的本质:H0到底正不正确？

首先，回顾A/B测试中的两个假设：

原假设（Null hypothesis, 也叫H0）：我们希望通过实验结果推翻的假设。 备择假设（Alternative hypothesis, 也叫H1）：我们希望通过实验结果验证的假设。

统计学中有两类错误：

• 一类错误（Type I error)：冤枉好人，即A有提升但是我们错误地认为此算法无效。我们把第一类错误出现的概率用α表示。这个α，就是Significance Level。

在做A/B测试的时候，我们希望第一类错误越低越好。实际操作中，我们把α人为定一个上限，一般是5%。也就是说，在做实验的时候，我们都会保证第一类错误出现的概率永远不超过5%。

• 二类错误（Type II error)：漏网之鱼，用β表示。根据条件概率的定义，可以计算出β = 1 - Statistical power。

一般情况下对两类错误上限的选取（α是5%，β是20%），我们可以了解到A/B实验的重要理念：宁肯砍掉4个好的产品，也不应该让1个不好的产品上线。

2.2.5.2.2 Baseline rate

这个看的是在实验开始之前，对照组本身的表现情况，对应T检验中的均值。在我们的实验里，baseline就是红色按钮的历史点击率。从直观上我们可以这么理解baseline： 当baseline很大（接近1）或者很小（接近0）的时候，实验更容易检测出差别（power变大），如果保持power不变，那么所需要的样本数量变小。举个例子，假设红色按钮的点击率是0%。那么，哪怕绿色按钮只有一个用户点击，相对于对照组来说也是挺大的提升。所以即便是微小的变化，实验也会更容易地检测出来。 同理，当baseline居中（在0.5附近徘徊）的时候，实验的power会变小。

这个参数完全是历史数据决定的。在我们的实验中，我们假定，实验开始之前的历史点击率是15%。所以Baseline Rate=15%。

此值用于确认上诉公式中的$\sigma$方差估计量

$$\sigma=\bar e=e_1(1-e_1)+e_2(1-e_2)$$

其中$e_1=$ Baseline rate

$e_2=$ Baseline rate+Minimum Dtectable Effect

2.2.5.2.3 Minimum Detectable Effect

顾名思义，这个参数衡量了我们对实验的判断精确度的最低要求。 参数越大（比如10%），说明我们期望实验能够检测出10%的差别即可。检测这么大的差别当然比较容易（power变大），所以保持power不变的情况下，所需要的样本量会变小。参数越小（比如1%），说明我们希望实验可以有能力检测出1%的细微差别。检测细微的差别当然更加困难（power变小），所以如果要保持power不变的话，需要的样本量会增加。

在工作中，这个参数的选定往往需要和业务方一起拍板。在我们的实验中，我们选定Minimum Detectable Effect=5%。这意味着，如果绿色按钮真的提高了点击率5个百分点以上，我们希望实验能够有足够把握检测出这个差别。如果低于5个百分点，我们会觉得这个差别对产品的改进意义不大（可能是因为点击率不是核心指标），能不能检测出来也就无所谓了。

2.2.6 增加p值显著速度

根据上述样本量估计及第一章介绍的假设检验原理计算，我们知道随着检测天数增多，样本量增大。P值会慢慢收敛，直到接近0.05以下实验成立。

但是在互联网行业的快速迭代中，快速的收敛，即通过更短的天数得到准确的结果，是我们所需要的。根据公式我们有三个思路使得AB实验快速得到显著结果：

• 上线对指标影响较大的策略，然而多数情况下这种策略可遇而不可求
• 增加实验的样本量，应该是普遍用的最多的，既然需要样本的总量固定，那么可通过提高每日实验流量配比让且更快速地收敛
• 缩减指标的方差，根据前面样本量计算和显著性检验介绍的公式可以知道，指标方差越小，所需样本量越小，也越容易统计显著

2.2.6.1 降方差（Variance Reduction）

AB测试根据大数定理和中心极限定理，大都符合下图分布。而不显著的核心原因之一就是方差太大。如果有办法能够降低方差，那实验结果自然更容易显著一些。

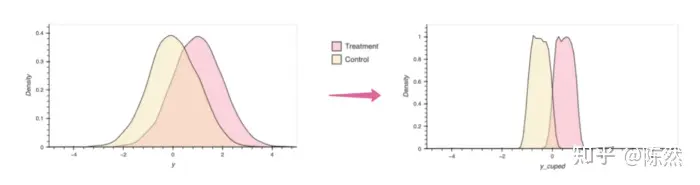
2.2.6.1.1 CUPED降方差

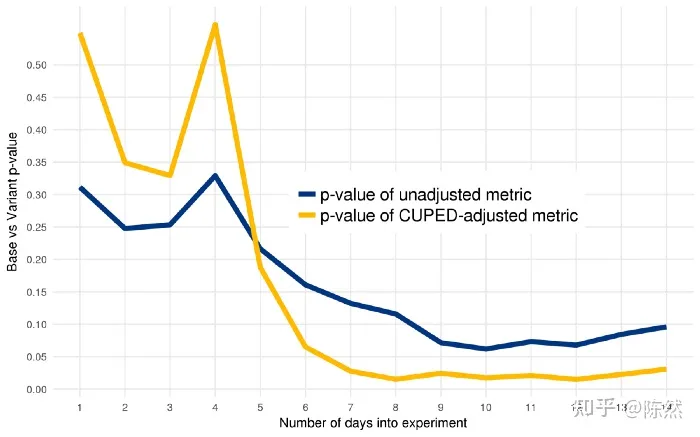
CUPED（Controlled-experiment Using Pre-Experiment Data），是一种利用实验前的数据来缩减指标方差，进而提高实验灵敏度的方法。由微软2013年发表。Netflix2016年进行多种降方差方法的case study实验，此种方法效果最好。 下图是Netflix的实验结果，黄色的CUPED调整过的在第7天就完全收敛到0.05以下，此时未调整过的p值仍有0.13左右无意义。

下面我们来介绍CUPED的原理和实现方法。 CUPED的核心思路是构造了一个新的指标，假定实验原来观测的指标为Y，新的指标为$Y_{cv}$（cv表示control variable）。

$$\hat{Y_{cv}} = \bar Y - \theta \bar X + \theta EX$$

其中 $\theta$ 是任意实数。由于$- \theta( \bar X) + \theta E(X)=0$那么$\hat{Y_{cv}}$ 是$E(Y)$的无偏估计。构造出来的Ycv有很好的特性，一是Ycv的均值是我们实验关注的指标Y的无偏估计，二是Ycv的方差小于原来指标的方差。

$ \hat {Y_{cv}} $的方差是：

$$\begin{aligned} var(\hat{Y_{cv}})&=var({\bar{Y} - \theta \bar{X}})\&=var({{Y} - \theta {X}})/n\&=\cfrac{1}{n}(var(Y)+\theta ^2 var(X)-2\theta cov(Y,X)) \end{aligned}$$

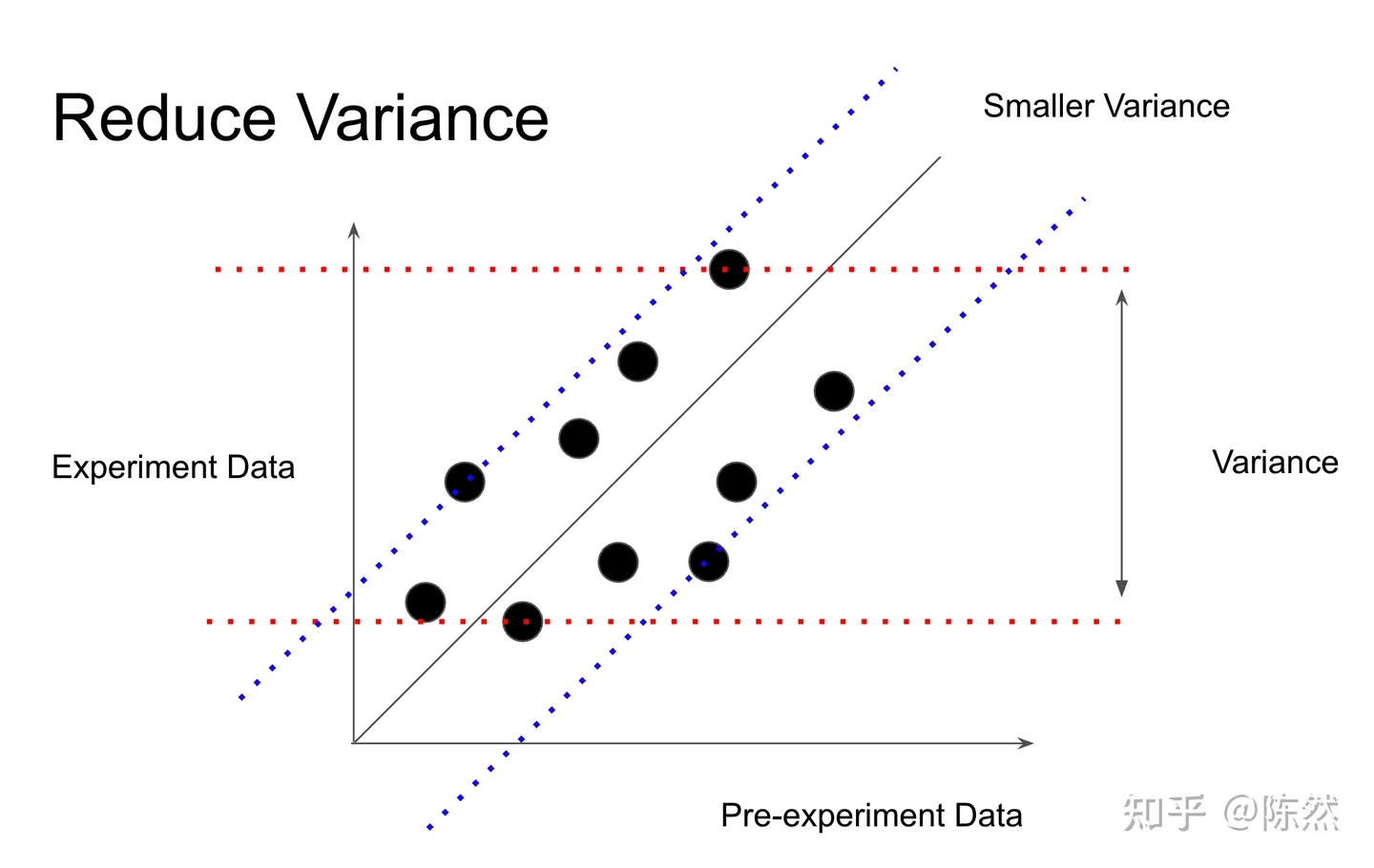
根据上述公式，我们发现当$\theta = cov(Y,X)/var(X)$时，我们构建出来的$\hat{Y_{cv}}$方差最小，而最小的方差则是$var(\hat{Y_{cv}} )=var(\bar Y)(1- \rho ^2)$。

此公式中$\rho = cor(Y,X)$是Y和X的协方差。故协方差越大，降方差的效果越好。

此时问题就集中在我们怎么的到这个和Y协方差大的协变量X，我们需要保证所选的这个变量不会受实验策略的影响，且与Y非常相关。多数情况下我们会选择实验前的此指标数据。如果是新用户或活跃频次等原因某些用户无实验前数据，那么微软论文提到可以再引入一个二元协变量，来表示该用户是否在实验前所选周期内出现了。不过Booking.com用的是另一个处理方法，是采用实验前指标的均值来填充那些在实验前所选周期未出现用户的指标的值。

当然我们除了实验前数据，可以选择实验期间的数据，只是一定要保证所选的这个变量不会受实验策略的影响。比如用户首次进入实验的所属当天星期几就可以作为一个协变量。另外，任何在实验策略效果生效前的实验期间的数据都满足不受实验策略影响的限制，因此都可以作为协变量，尤其是实验策略生效比例极低的情况下，这些数据用来做协变量可能会很有用。

非用户级别指标的处理方法。因为前面假设实验的基本单元和指标计算的基本单元是用户，如果实验指标的计算单元更细，比如CTR，那么需要delta method和方差缩减一起使用。这时候协变量也就不止限于用户级别数据了，更细粒度如页面级别也是可以的。

此时我们再回忆一下，降方差的公式及图形展示。

$$CUPED-adjusted metric = Y - \theta (X - \bar X)$$

$$\theta = cov(Y,X)/var(X)$$

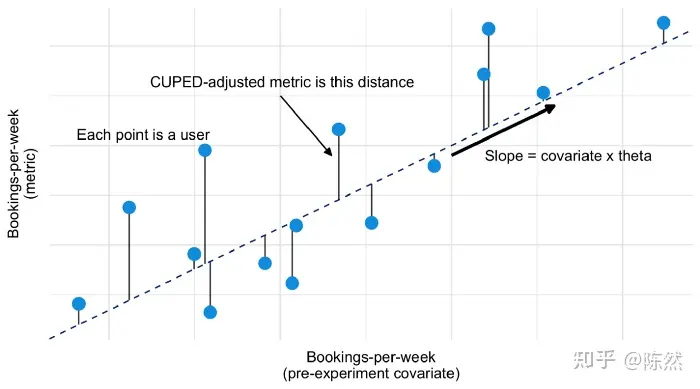
2.2.6.1.2 Stratified Sampling

2.2.6.1.3 Post Stratification

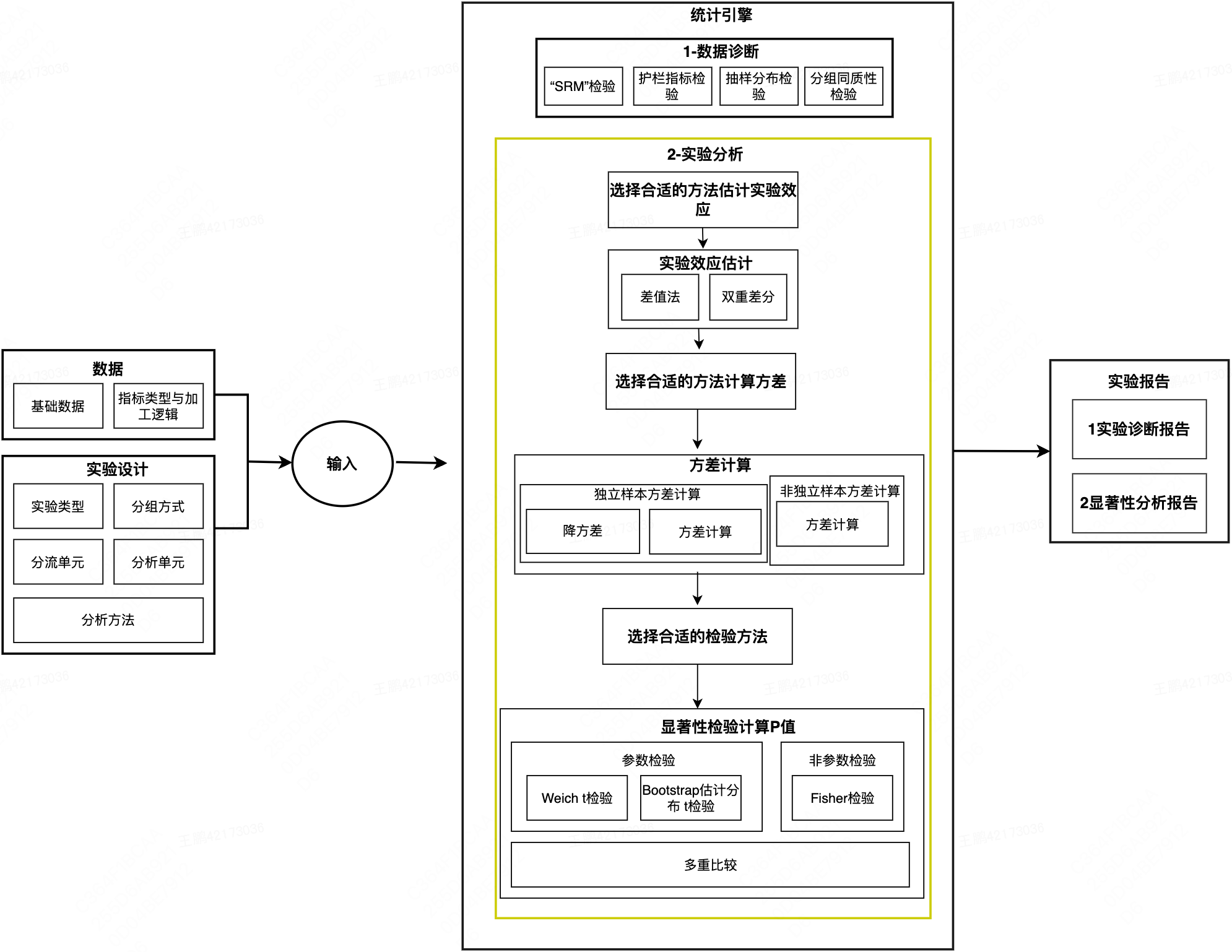
2.3 统计引擎

2.3.1 数据诊断

分析环节的数据诊断，旨在提醒实验者注意可能违反实验假设的情况。很多人认为实验一定按照设计运行，实际上这一假设失败的概率远高于人们的预期。失败实验的分析结论通常是有严重偏颇的，甚至一些结论是完全错误的。在输出显著性分析报告之前，通过护栏指标检验，确保业务不会因策略的迭代受到伤害，通过分组同质性检验、“SRM”检验查看实验执行是否符合预期，确保实验本身的可信度，抽样分布检验，为后续选择合适的显著性检验方法提供依据。

2.3.2 选择效应估计方法

自动选择与数据和实验设计匹配的分析方法，避免统计陷阱。根据分组方式，提供了差值法和双重差分两种效应估计方法。

2.3.2.1 差值法

对于完全随机分组可以直接进行两组值的比较。

2.3.2.2 DID双重差分

上文中提到，除了完全随机分组，准实验需要通过DID双重差分规避由于无法完全随机分组造成的组间差异。

2.3.2.2.1 DID双重差分介绍

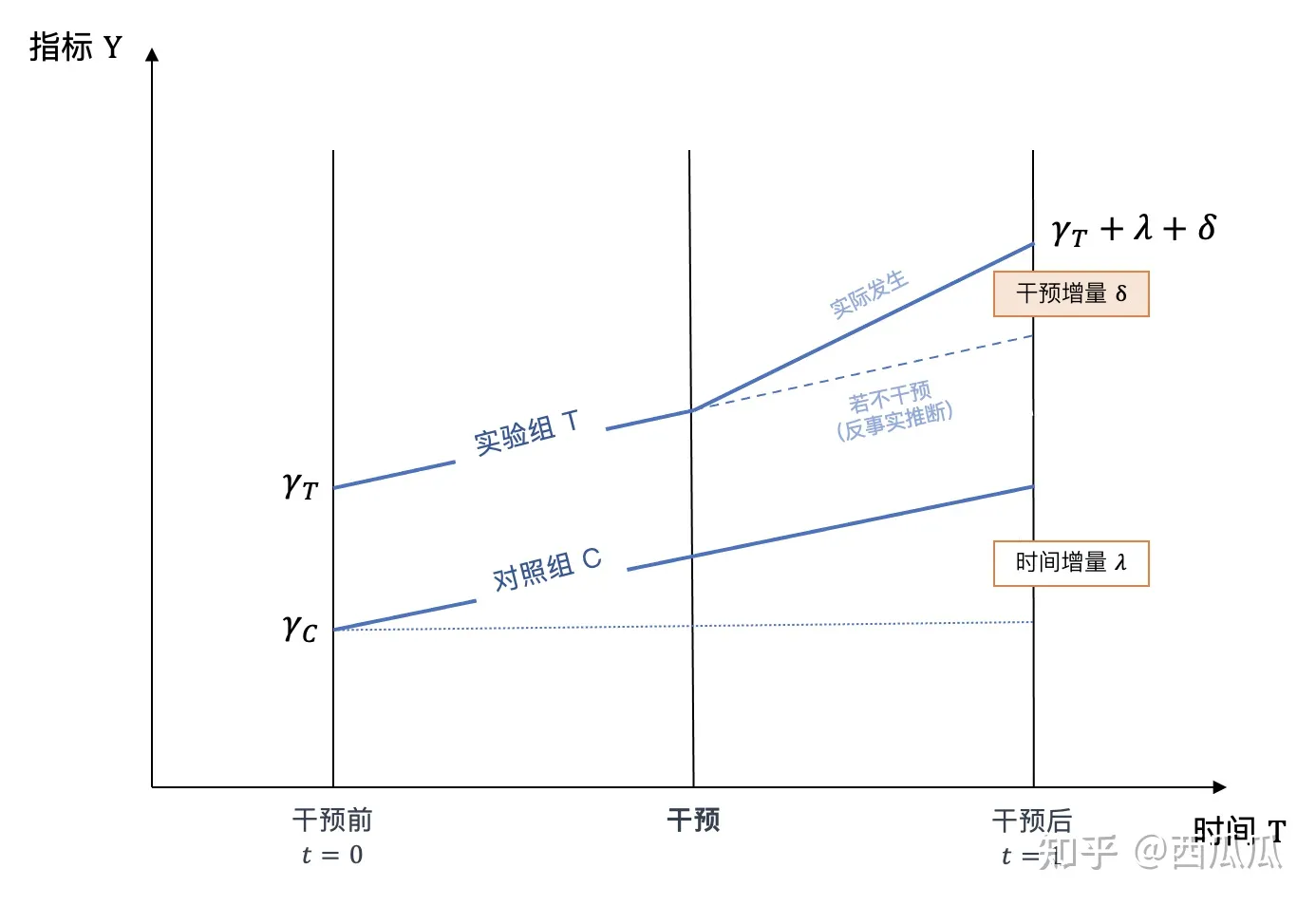
步骤：

• 分组：对于一个自然实验，其将全部的样本数据分为两组：一组是受到干预影响，即实验组；另一组是没有受到同一干预影响，即对照组；
• 目标选定：选定一个需要观测的目标指标，如购买转化率、留存率，一般是希望提升的KPI；
• 第一次差分：分别对在干预前后进行两次差分（相减）得到两组差值，代表实验组与对照组在干预前后分别的相对关系；
• 第二次差分：对两组差值进行第二次差分，从而消除实验组与对照组原生的差异，最终得到干预带来的净效应。

$$y_{it}=\alpha + \delta I(s(it)=s) + \gamma_{s(i)} + \beta_t +\epsilon_{it}$$

其中$s(i)$代表个体所属的组别（实验组/对照组），$\gamma _{s(i)}$代表干预前的量级，$\beta _i$捕捉处理组与控制组的固有差别，$\lambda _t$代表干预后的自然增量($\lambda _0=0$)，$\delta$代表干预带来的增量，$I(…)$是指示函数，当其中的等式$s(i)=s$成立时取值为1、否则为0。

通过最小二乘法OLS估计，我们需要计算的干预带来的增量$\delta$即实验组干预前后的均值的差减去对照组干预前后均值的差：

$$\delta=(\bar y_{T,1} - \bar y_{T,0})-(\bar y_{C,1} - \bar y_{C,0})$$

2.3.2.2.1 DID双重差分需要满足的假设

通过前面的描述可以看到，双重差分法的计算过程很简单，即实验组干预前后的均值的差减去对照组干预前后均值的差。但若希望得到的结果是准确的，对应的样本数据需要满足下面三个假设：前两个假设使用时通常会满足、无需专门验证，需要重点验证第三个假设。

2.3.2.2.1.1 线性关系假设

该假设来自于线性回归，认为因变量（Treatment）与结果变量存在线性关系。

2.3.2.2.1.2 个体处理稳定性假设

（The Stable Unit Treatment Value Assumption，SUTVA）

个体的outcome是取决于个体干预变量treatment的一个函数，该假设由两部分组成

• 一致性（Consistency）：个体接受处理后所导致的潜在结果是唯一的。

例：我养狗了会变开心，无论是什么狗、不存在因为狗是黑的就不开心

• 互不干预（No interference）：个体接受处理后导致的潜在结果不受其他个体处理的影响。

例：我在淘宝上领到了红包之后会更愿意买东西，不因为我同事也领了红包就意愿降低了

2.3.2.2.1.3 平行趋势假设

（Parallel Trend Assumption）

定义：实验组和对照组在没有干预的情况下，结果的趋势是一样的。即在不干预的情况下，前后两个时间点实验组与对照组的差值一致。

检验方式：通常情况下我们可以通过画图或者按照定义计算的方式验证样本是否满足假设

这个假设在随机实验下，通常是满足的，因为两批用户是很近似且同质的用户。但在观察实验的情景下，有可能会不满足，此时不能简单粗暴、不加处理的直接使用DID，需要对模型或数据进行处理。

2.3.2.2.1.3.1 对模型处理：

2.3.2.2.1.3.1.1 经典DID模型

在传统DID模型上控制了个体固定效应（individual fixed effects）和时间固定效应（time fixed effects），并去除单独变量。模型如下：

$$y_{it}=\alpha + \delta I(s(it)=s) + u_{s(i)} + \lambda t +\epsilon{it}$$

其中$u _{s(i)}$为个体固定效应，加入个体固定效应后，就不必再放入处理组虚拟变量\gamma _{s(i)},否则会引起多重共线性问题。因为前者包含比后者更多的信息（前者控制到个体层面，而后者仅控制到组别层面）。 其中$\lambda_t$为时间固定效应，同理,加入时间固定效应就不用再加处理期虚拟变量（post t）。否则，将导致严格多重共线性，因为前者包含比后者更多的信息（前者控制了每一期的时间效应，而后者仅控制处理期前后的时间效应）

后仍使用最小二乘法OLS，根据聚类稳健标准误（cluster-robust standard errors），进行拟合得到系数$\delta$。

例：

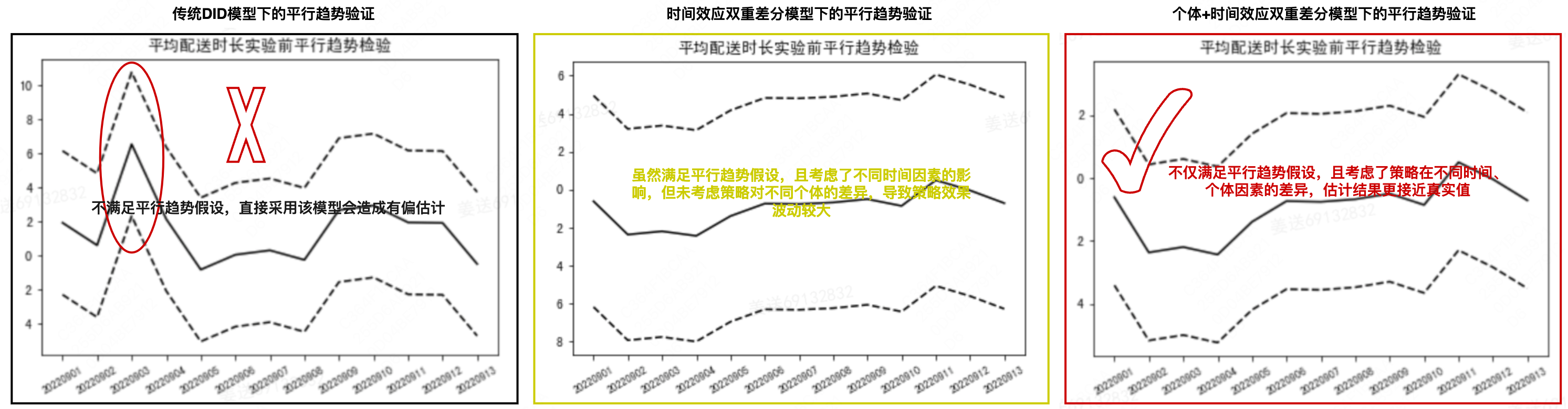
根据上图所示，在当前的业务场景下，并不满足传统DID模型的平行趋势假设，如果贸然使用，会造成估计偏差，时间效应的双重差分模型和个体+时间效应的双重差分模型，虽然都满足平行趋势假设，但从实际置信区间看，后者因为考虑了策略对不同个体的差异，波动较小，估计结果更加接近实际值，所以应采用后者。

2.3.2.2.1.3.1.2 异时DID

在传统与经典DID的模型设定中，一个隐含假设是，处理组的所有个体开始受到政策冲击的时间均完全相同。但有时也会遇到每位个体的处理期不完全一致的情形（heterogeneous timing）；比如，某项试点政策在不同城市分批推出。此时，可使用“异时DID”（heterogeneous timing DID）。

异时DID的关键在于，既然每位个体的处理期不完全一致，则处理期虚拟变量也因个体而异，故应写为post(i,t)，既依赖于个体 i，也依赖于时间 t。

2.3.2.2.1.3.1.3 广义DID

以上各种DID方法均假设存在处理组与控制组的区别，但有时某项政策在全国统一铺开，此时只有处理组，并没有控制组，是否还能使用DID呢？答案是“能”，可以尝试“广义DID”（generalized DID）。

使用广义DID的重要前提是，虽然所有个体均同时受到政策冲击，但政策对于每位个体的影响力度并不相同，不妨以 intensity（i） 来表示。

2.3.2.2.1.3.1.4.异质性DID

传统的处理效应模型一般假设“同质性处理效应”（homogeneous treatment effects），即所有个体的处理效应都相同。显然，此假定太苛刻，在实践中难以成立。更为合理的假定则为“异质性处理效应”（heterogeneous treatment effects），即允许每位个体的处理效应不尽相同。具体而言：

1）在DID的框架下，引入异质性处理效应，即在于对交互项（treatpost）的调整，即引入在组别上的交互项（treatpost*group）。

2）模型建立上，在经典DID的模型中，再引入三重交互项 ，构建异质性DID模型。

2.3.2.2.1.3.1.5 三重差分法

（Difference-in-differences-in-differences, DDD） 定义：再做一次双重差分消除实验与对照组差异带来的增量，剩下的即干预带来的增量。

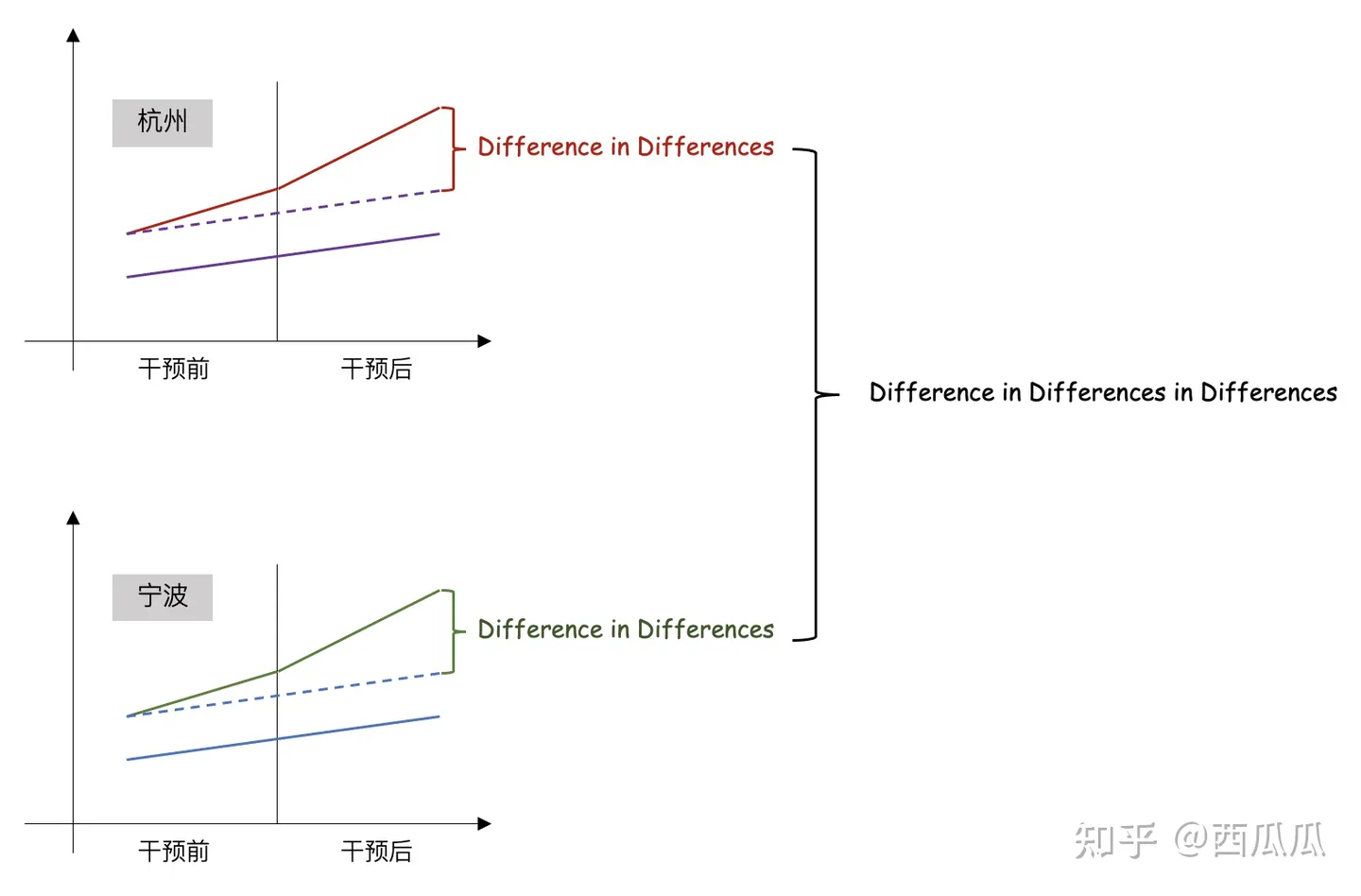
三重差分的概念比较抽象，这里通过一个例子来说明：

背景：假设淘宝针对杭州的学生（实验组）发放红包，其他人不发。如果想衡量红包带来的转化增量，直观的会选用杭州的非学生作为对照组。但由于学生和非学生的购买力和趋势本身具有差异，此时平行趋势假设无法满足。 解决方案：此时我们可以引入一个其他的城市，譬如宁波。计算宁波学生与非学生的DID，可以认为这里的DID是来自于人群差异的增量；最后我们用杭州的DID减去宁波的DID则得到发红包带来的净效应。

2.3.2.2.1.3.2 对数据处理

当前常用的处理方式由如下三种：倾向得分匹配（Propensity Score Matching，PSM）、三重差分法（Difference-in-differences-in-differences, DDD）、合成控制法（Synthetic Control Method）。可以理解为人工构建相对同质的实验组和对照组的方法。

2.3.2.2.1.3.2.1 倾向得分匹配

相对于后两种方式，该方法在工业界更常用。 目的：从干预的人群和未干预的人群里找到两批人符合平行趋势假设 业务理解：在这两个人群里找个两批同质的人（该场景下的同质：在treatment维度上有近似表现的人）

例子：在探究领取红包对用户购买行为影响的场景下，对用户领取红包的倾向做预测（打分），认为分数相近的用户是matching、即同质的。圈选出分数相同的用户之后再验证平行趋势假设。 完成PSM后数据会呈现一些规律（如图所示）：

干预人群与非干预人群的score分布 —— 匹配后分布一致

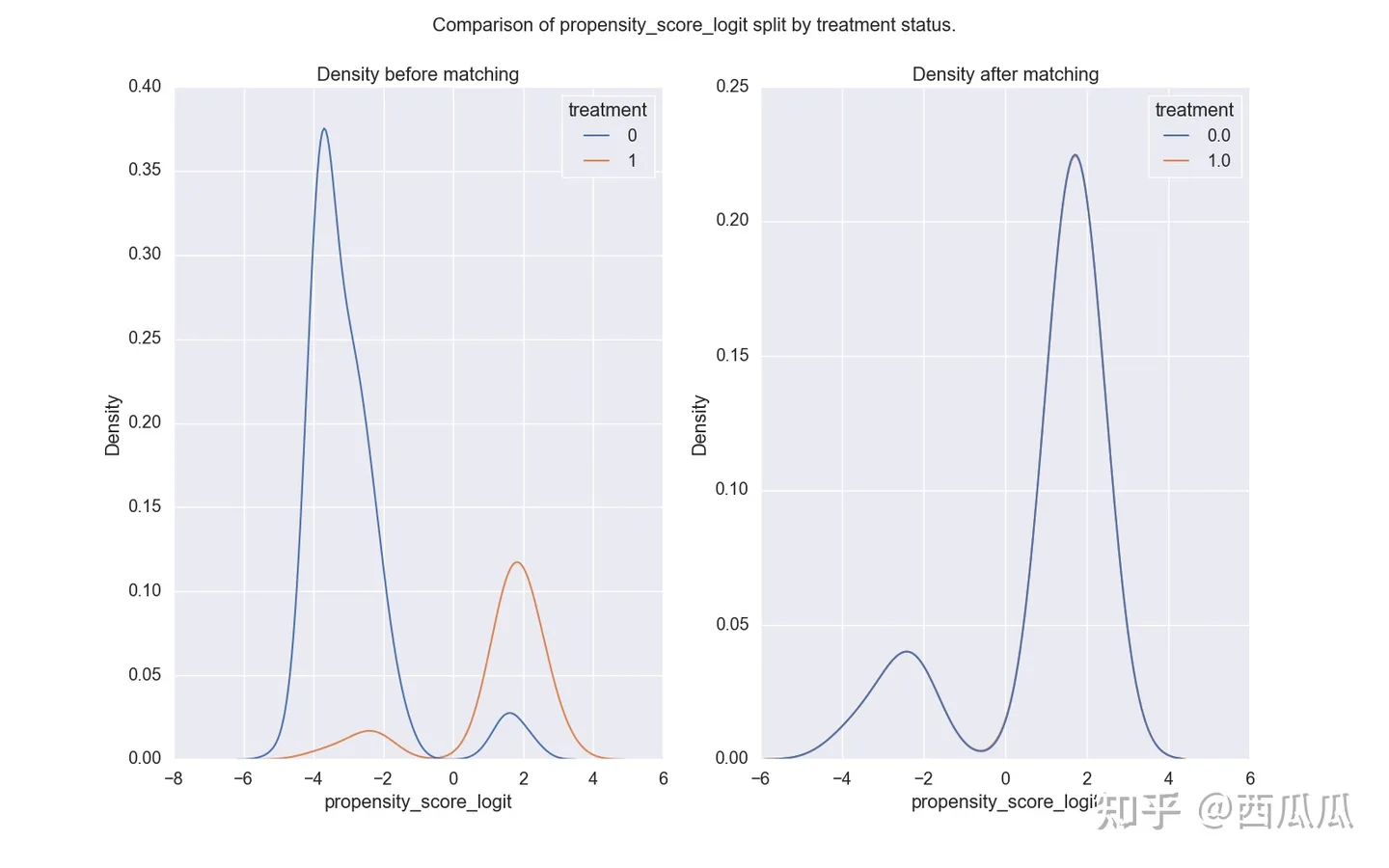
抽样后人群在一些画像（如年龄、性别、职业）上的分布会更接近，这间接验证了两组人群更为相似（同质）。但我们需要注意的是，通常情况下不能直接根据用户画像去圈同质人群，因为属性分布相似只是propensity score相似的一个必要条件，而不是完全条件。且属性多种多样并不容易进行判断及决策。

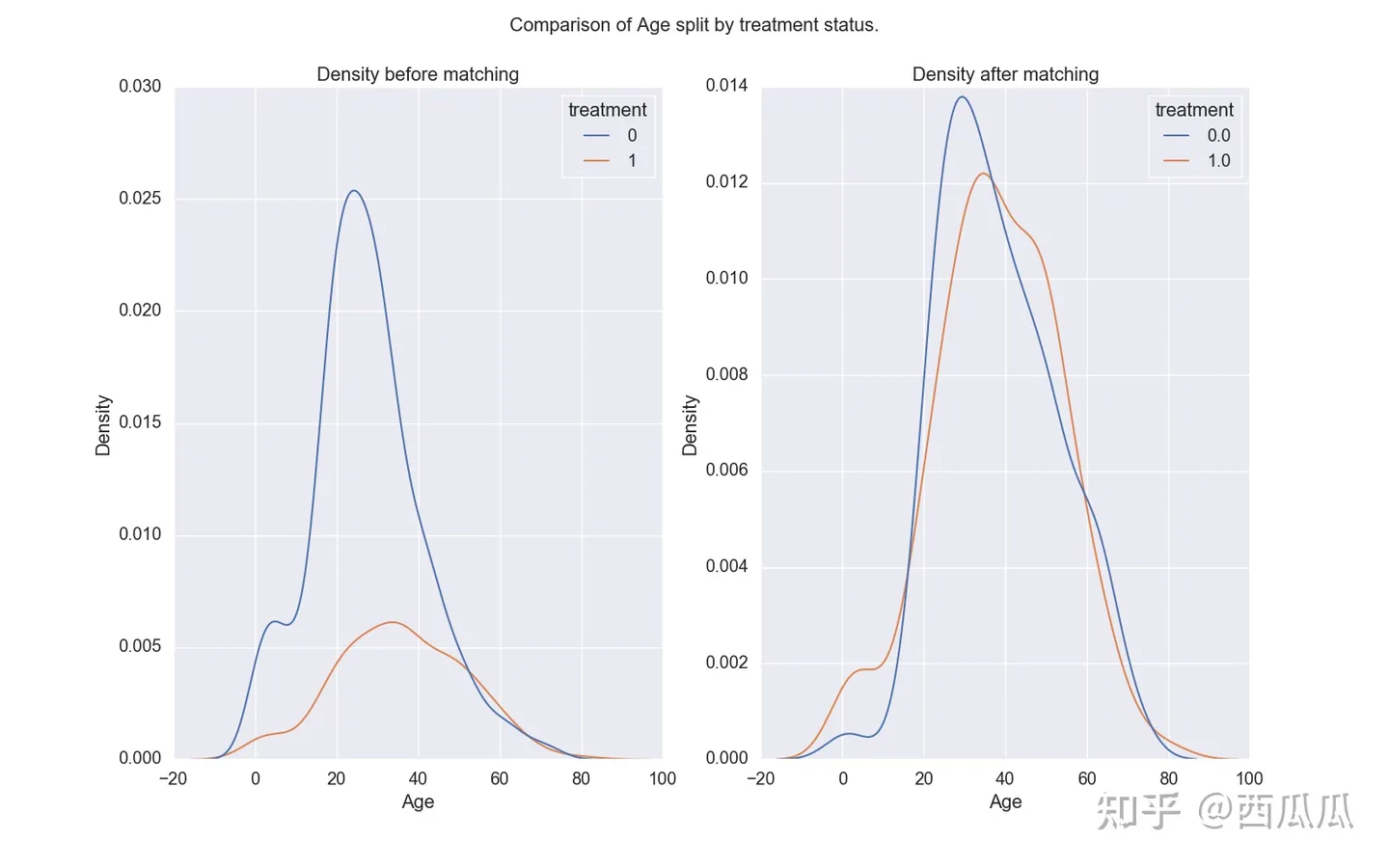
2.3.2.2.1.3.2.2 合成控制法

多用于城市政策的结果估算。 定义：通过对其他对照组加权，构造出一个虚拟的对照组，使其满足假设。

例：探究消费券对杭州市民的影响，取20%上海市民、30%南京市民、50%合肥市民构建一个虚拟的、与杭州类似的对照组。 为了使虚拟对照组与干预组更接近，需要求解最优的权重组合 ，使得虚拟对照组与实验组最相似。

值得一提的当随机分流的量级不一致时，也可能会导致不同质，因为量级越大存在多个user_id对应一个自然人的情况越多，会影响user_id粒度的指标统计；

检验同质性的方法：对于一般的AB分流，我们可以通过分流后两组人群在性别、年龄等属性上分布的相似度来检验同质性。

2.3.4 方差计算

2.3.4.1 方差错误导致统计陷阱

如果不能正确的估计方差，那么P值和置信区间都将是错的，这些错误会导致我们通过假设检验得到错误的结论。高估的方差会导致假阴性，而低估的方差会导致假阳性。下面是几个估计方差时的常见错误。

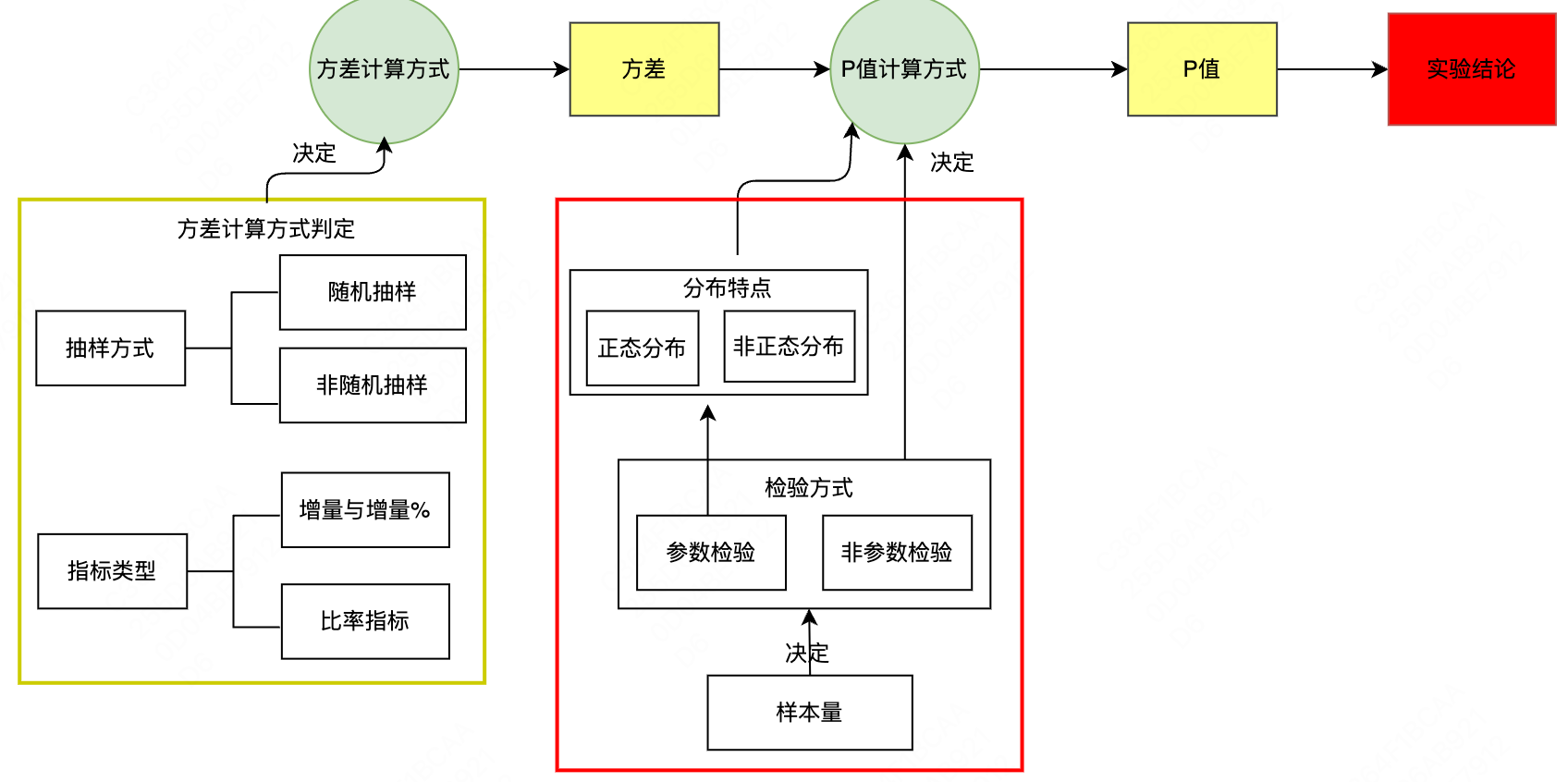
2.3.4.2 正确计算方差的方法

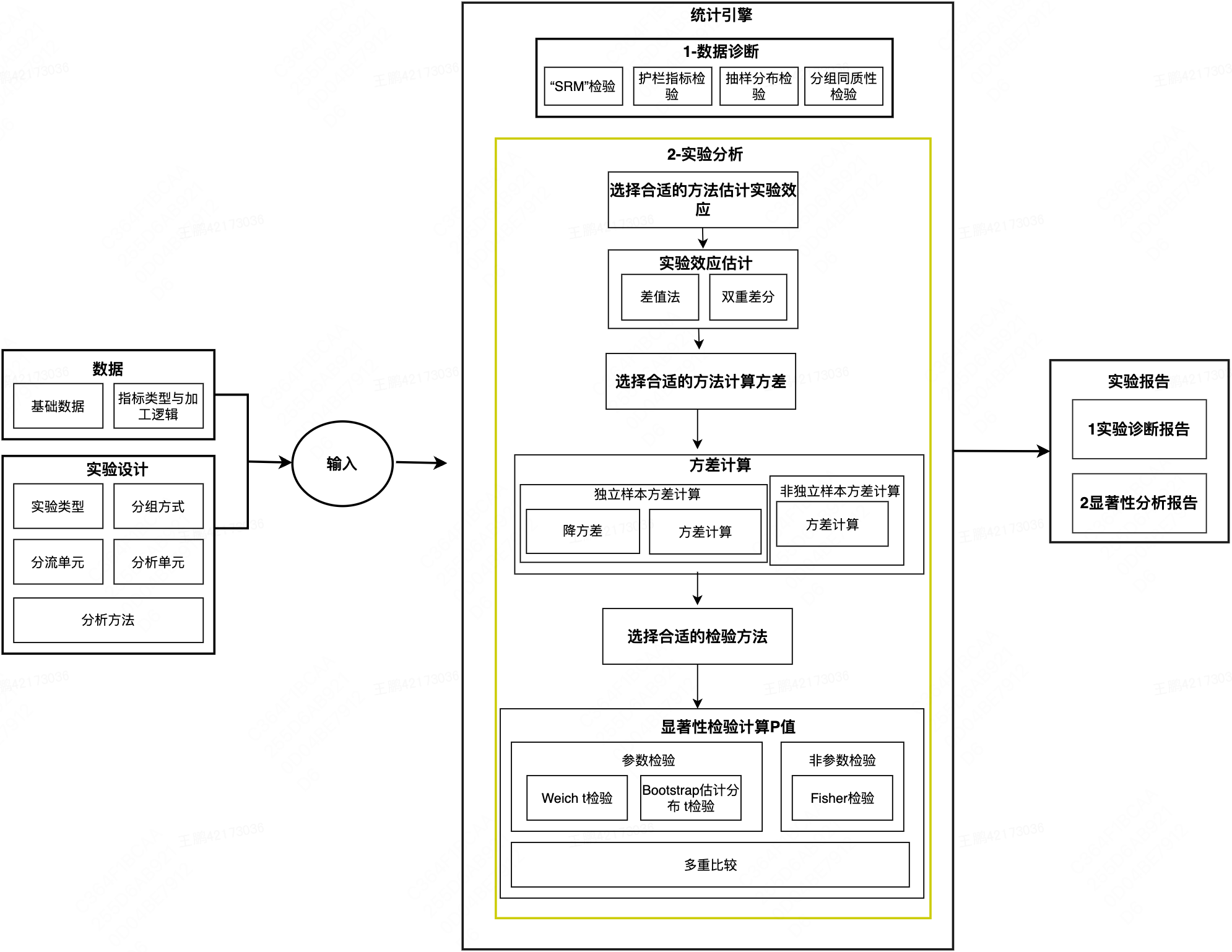
方差计算根据是否随机抽样，将其分为独立样本方差计算和非独立样本方差计算，独立样本方差计算，根据指标是增量提升还是相对提升和分流单位与分析单位是否一致综合因素，提供了直接计算和Delta方法计算，避免方差计算陷阱，非独立样本，通过模拟数据的实际分布，给出方差的准确计算。

2.3.5 p_value显著性检验

2.3.5.1 p_value检验陷阱

容易忽视的检验方式导致的P值计算陷阱：统计学对于多大样本量即可认为中心极限定理成立并没有完全的定论，并非所有大样本场景下的样本分布都满足正态性假设，避免有偏样本采用默认正态分布下的检验方法。Weich t假设检验是参数检验常用的一种检验方法，其本质上假定实验组、对照组样本均值等的渐近正态性成立，该理论实际上是建立在大样本情形下的中心极限定理基础上。统计学对于多大样本量即可认为中心极限定理成立并没有完全的定论，这实际上也取决于原始分布本身偏离正态分布的程度。

从经验来看，若样本仅稍微偏离正态总体，大于30的样本量或许就足够了。然而对于有偏样本，Ron Kohavi等(2014) 指出当样本偏度大于等于1时，一个经验准则便是只有计算样本均值的观测样本量大于$355 s^2$时才可认为中心极限定律成立。实际抽取了一个样本量为13832的活动实验，其实验组、对照组差值的抽样分布呈现右偏，不符合正态分布，如下图所示：

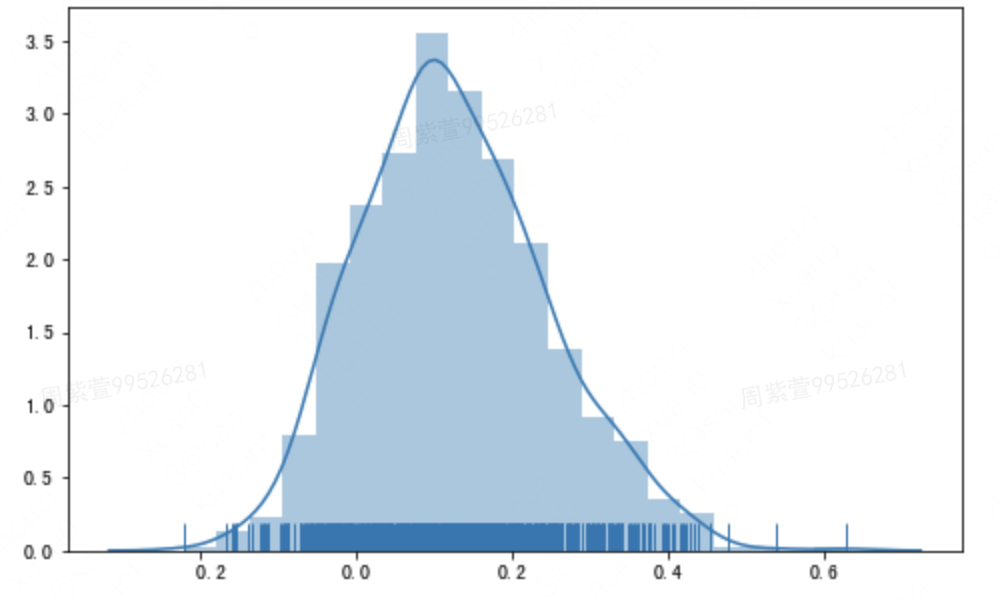
如果所有场景下默认采用正态分布情形下的检验方式计算P值，容易导致错误的P值计算。

2.3.5.2 p_value检验方式

样本量小于30的超小样本下，采用非参的Fisher检验以满足功效要求，在样本量大约1万的超大样本下，接受检验统计量的渐近正态性成立并采用Weich t假设检验；在样本量大于30小于1万下，进一步样本实际分布情况，如果统计量渐近正态性成立，则采用Weich t检验，如果不成立，采用Bootstrap估分布进行统计推断。

三.AB测试的一般人员分工

谈到实验部分，我们就不得不先介绍一下业界有关AB测试的工作分工。 在工作中，AB测试一般由数据科学家主导，配合算法工程师和后端工程同学，数科同学在策略迭代之初，就参与到算法年度目标的讨论中，辅助算法一起制定量化策略好坏的综合评估指标，并基于场景特点选择合适的实验方法，完成对应场景下的实验设计，后端工程同学，负责将新方法集成到实验平台，作为公共能力为用户提供服务。

我们将整个流程分为三个阶段：构建想法，通过AB实验验证想法、沉淀知识库形成实验记忆。

构建想法是实验的输入阶段，构建想法的质量直接决定了实验的效果，如果这个阶段构建的想法不够好，那么AB实验阶段只能起到验证错误的作用，降低犯错误的概率，无法带来增长。

验证想法就是实践AB实验的过程，可以分为实验假设、实验设计、实验运行、实验分析和实验决策五个关节，实验假设环节，即形成实验目标，构建综合评估指标，实验设计，基于场景约束，选择合适的实验方法。

最后，通过Launch Review发起实验决策；将成功和失败的案例沉淀下来，形成实验记忆，不仅可以帮助我们发现策略的通用性，而且有助于帮助我们从失败中寻找机会。

四.AA测试

不同与在A/B测试中是使两个不同页面来进行实验。在A/A测试中，两组用户被分配到两个完全相同的页面组，那为什么要用两个完全相同的页面来做实验？这是因为A/A测试的实验目的并不是为了发现两个版本是否会带来转化的提升，而是为了验证两组实验用户之间是没有显著差别的。

当公司采用新A/B测试工具时，会选择先完成A/A测试。A/A测试可以为他们提供如下3大帮助：

• 检查A/B测试工具的准确性 在A/A测试中，当实验组和对照组之间绝对没有差异时，那么就可以判断两组用户在关键维度上是一样的、不会对接下来的A/B测试产生混淆与干扰因素。但是，当A/A测试在两个相同变体之间产生了获胜者的情况下，那后续的A/B测试的结果就会是有问题的。

在互联网工程中，数据科学家们常常通过模拟几百次AA实验，查看关注指标的P值是否在0到1之间均匀分布，的方法确认实验方法的可靠性。下表是美团在随机轮转实验中，引入入Fisher和Neyman检验时的模拟验证。

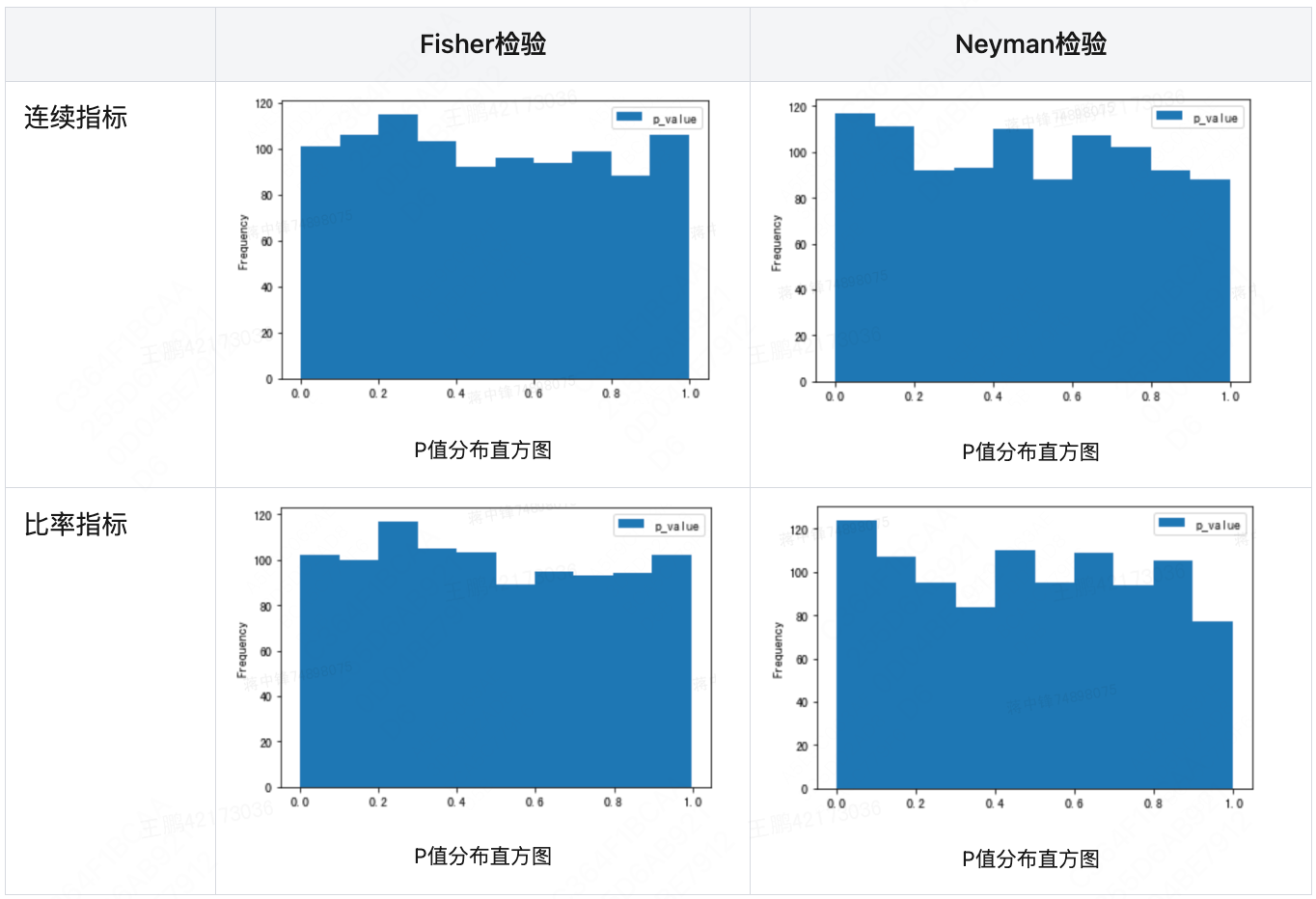
• 为将来的A/B测试设置基准转换率 需要知道将要用作与结果进行对比的基准转换率。A/A测试可以帮助设置网站的基准转化率。让我们来看看这个示例：假设正在运行一个A/A测试，其中实验组A在10,000个访问者中产生了303个转换，而相同的对照组B在10,000个访问者中给出了307个转换。当两个版本之间没有差异时，A的转换率为3.03％，B的转换率为3.07％。因此，将来A/B测试的基准转换率范围可以设置为3.03-3.07％。如果A/B测试的实验组结果是在这个范围内的，那就说明在A/B测试中的实验组和控制组没有显著差异。

• 确定最小样本量 如上章最小样本量确认的公式，AA测试可以帮助我们实验并初始基准转化率及判断精确度的最低要求。Avast的A/A测试进行了12天，他们从中获得了很多数据。总体来看，该测试涉及超过1000万用户和6500笔交易。在“免费”细分中，他们看到转换率差异为3％，平均订单价值（AOV）差异为4％。在“付费”细分中，他们看到了2％的转化率差异和1％的AOV差异。（注意，以上结果是A/A测试结果，A/A测试的目的是为了证明结果没有显著差异。） “所有这些差异在统计数据上都是不显著的，” Michal说。他补充说：“鉴于A/A测试的这些结果，我们设定了内部A/B测试的阈值。例如，如果A/B测试的转换率或AOV的差异小于5％，我们就需要注意这个提升不是实验操纵的结果，而是偶然的。”

五.生产上多种多样的AB测试

通过上方的基础介绍我们已经了解了传统AB测试。毋庸置疑AB测试是理论上最客观最准确的线上评估方法。但由于AB测试对于场景假设的要求过于严苛，如随机性、约束性等。除了上述提到的准实验外，在本章我会结合多互联网公司的实践场景进行AB测试的实际应用变体的拓展。

5.1 随机轮转实验

5.2 更高效的AB测试–interleaving

先随着我想象一个每时每刻都在互联网发生的场景，你是手机淘宝主页面的算法工程师，主页面由主图推荐、活动推荐和产品推荐等非常多的模块组成，这些模块都在持续的优化迭代，最令人担心的是，每个模块都会互相影响最终导致用户的决策。同时你负责的模块还有几十个算法待测验。你要怎么做AB测试，以在最快的时间内，不被其他场景实验影响保证准确性的情况下，判断出你手上的最优算法呢？

我们先分析这个场景下的问题：

1：在互联网场景下，非常活跃用户的数量是少数，但其贡献的点击、时长却占较大的比例，因此实验组和对照组中活跃用户被分在A组的多还是被分在B组的多，将对结果产生较大影响，从而掩盖模型的真实效果。对于这个问题，传统AB测试会按照活跃度分层抽样以保证AB两组之间活跃率相对平衡，但是可能引入其他维度的bias，这个要多方面看各要素的tradeoff了。而interleaving解决这个问题的思想则是不对测试人群进行分组，而是让所有测试者都可以自由选择A和B。在实验结束时，统计每个人可选择A和选择B的比例。这样就消除了AB组测试者自身属性分布不均的问题，也提升了用户选择的效率。

2：线上AB Test必然要占用宝贵的线上流量资源，当需要测试的备选场景、算法数量非常多时，例如近期同一页面有五个模块需要测试，需要做到互不干涉就需要把线上流量切分为5份，同时对于某个模块的算法研发侧，大量候选算法需要逐一进行AB Test，又会对流量进行切分几十到几百个。根据上一章AB测试样本量小节，样本需要达到一定量才有统计学意义。故大量的算法测试需求和有限的用户流量需这二者之间的矛盾必然愈演愈烈。这就迫切需要设计一个样本需求少且快速的线上评估方法。Netflix促生了以下的AB test的预先阶段来帮助从上百各算法中初筛出个位数的优质算法进入接下来准确的AB测试阶段。

为此，Netflix设计了一个两阶段的线上测试过程，如下图。 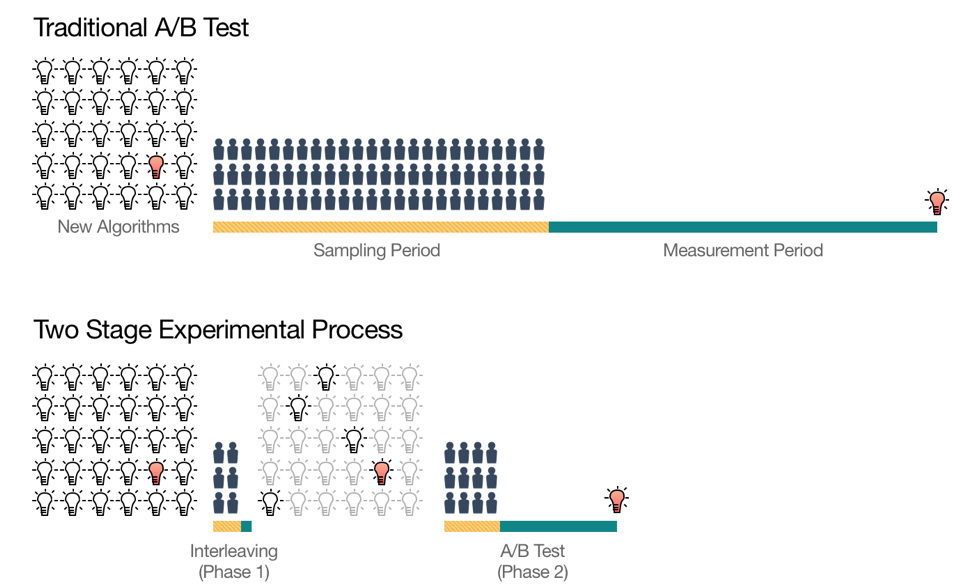第一阶段利用被称为Interleaving的测试方法进行候选算法的快速筛选，从大量初始想法中筛选出少量“优秀的”Ranking算法。 第二阶段是对缩小的算法集合进行传统的AB Test，以测量它们对用户行为的长期影响。

在Interleaving测试中，不分AB组，而是只有一组订阅用户，这些订阅用户会接受到通过混合算法A和B的排名生成的交替排名。这就使得用户同时可以在一行里同时看到算法A和B的推荐结果（用户无法区分一个item是由算法A推荐的还是算法B推荐的）。进而可以通过点击或计算观看时长等指标来衡量到底是算法A好还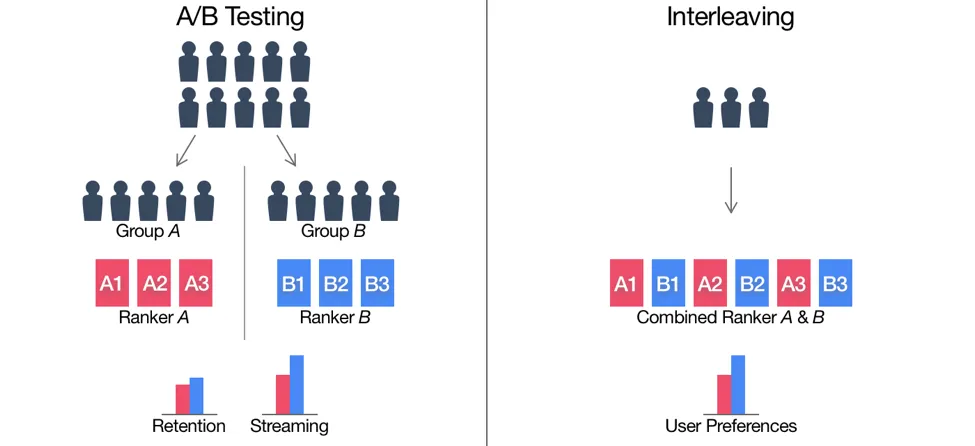是算法B好。 当然，在用Interleaving方法进行测试的时候，必须要考虑位置偏差的存在，避免来自算法A的视频总排在第一位。因此需要以相等的概率让算法A和算法B交替领先。这类似于在野球场打球时，两个队长先通过扔硬币的方式决定谁先选人，然后在交替选队员的过程。 底是算法A好还是算法B好。

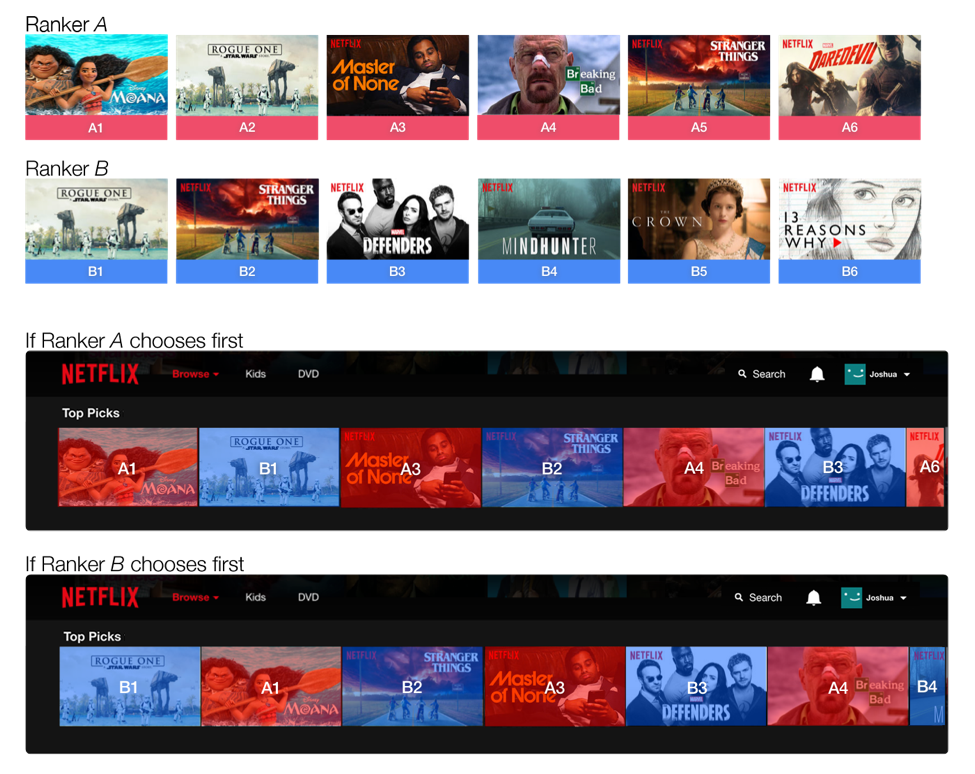
了解了interleaving具体是什么之后，我们回到最初我们提出的两个问题：高效性和准确性。 高效性： 判定算法A是否比算法B好的“错误”概率。可以看出的是interleaving的方法利用10^3个样本就能够判定算法A是否比B好，而AB test则需要10^5个样本才能够将错误率降到5%以下。这就意味着利用一组AB Test的资源，我们可以做100组Interleaving实验。这无疑大大加强了线上测试的能力。

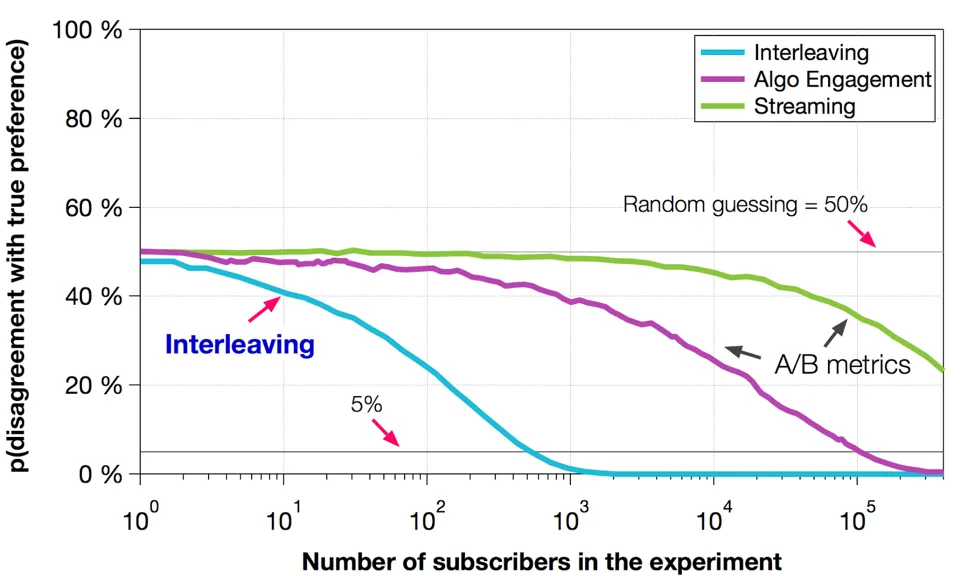
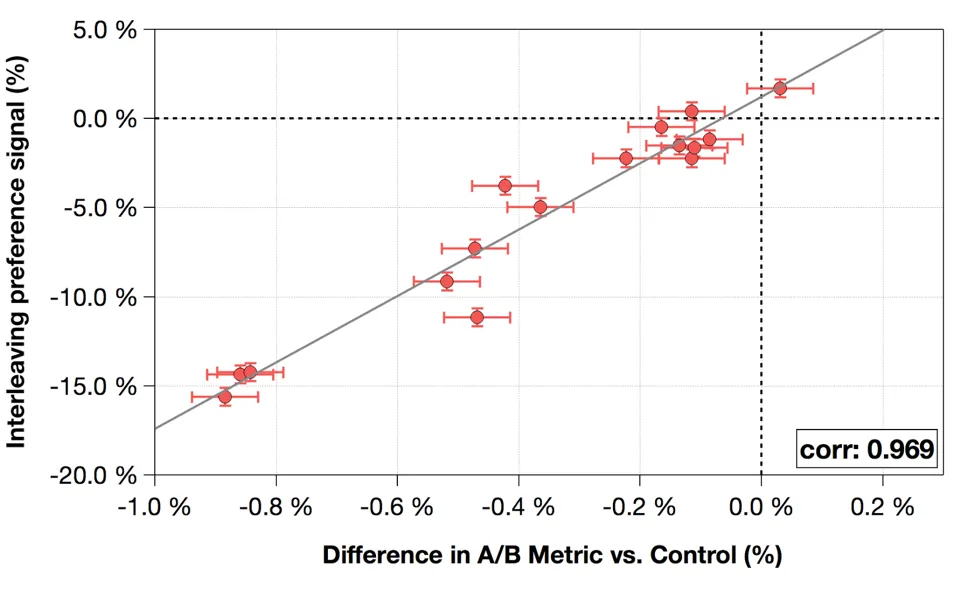
准确性： Interleaving中的实验指标与AB Test指标之间的相关性。每个数据点代表一个Ranking算法。 我们发现Interleaving指标与AB Test评估指标之间存在非常强的相关性，这就验证了在Interleaving实验中胜出的算法也极有可能在之后的AB Test中胜出。

总结 快速的本质是因为用户可以同时看到A和B时选择A，和只能看到A选择A的，信息量是不同的，所以可以通过1/100的少量用户就可以得到结果。 为什么不直接使用inter leaving的结果呢，因为从宏观看最终策略是A还是B，用户都只能看到A或B，而不是AB的混合，所以混合测验出的结果只能是参考，最终需要真实的单独策略模拟即AB测试。从统计看interleaving仍会有位置bias问题，比如一种ranking能够推出最好的top3，但是另一种ranking能够推出最好的top10。这两种混排在一起之后，受限于用户浏览深度，第一种看起来会好很多，但单独上线的指标说不定还是第二个好。所以interleaving只用于初筛，最终还是要用过传统ab test做最终验证。

5.3 用户裂变场景怎么避免污染

泛裂变社交是指通过社交工具在用户自有的圈子里进行一次或多次的传播，在很短时间内形成用户介绍用户的模式，从而在短时间内实现大量的用户增长及销售额增加。 裂变营销是把个人当成传播的媒介，把原本要给广告商的费用花在单个用户的身上，从而推动用户来帮忙传播。

理想情况下，AB实验中，实验组是能够参与策略玩法的用户群，对照组是不能参与策略玩法的用户群。但是现在普遍常见的泛社交裂变业务模式会使实验桶和对照桶互相影响，对AB增量的计算会产生一定的污染性，导致增量计算有所偏差，那么如何处理这种污染来还原真实的AB增量，需要一个科学的评估方案。

5.4 低响应场景