背景
不知道有没有人和我一样在学习乐器时好奇。
为什么do是do呢？
为什么是高八度，不是高六度呢，do和高八度的do有什么关系？
为什么和C间、E和F间是半音，而其他C和D、D和E等之间都是全音呢？
音高是连续的，人类以什么样的标准制造音阶以获得和谐好听的音乐？
这其中有没有类似于绘画中的“黄金分割律”的数学规律呢？
一.音的本质
音是振动产生的，音的属性具有对应的物理含义：音高（频率）、音长（时值）、音强（振幅）和音色（频谱）。其中，音高是音的主要属性。振动规则（周期性强）、容易区分音高（弥散度小）的音称为乐音，是音乐中的主角。
频率过高或过低的声音人耳不能感知或感觉不舒服，音乐中常使用的频率范围大约是 16~4000 赫兹，而人声及器乐中最富于表现力的频率范围大约是 60~1000 赫兹。
在弦乐器上拨动一根空弦，它发出某个频率的声音，如果要求你唱出这个音你怎能知道你的声带振动频率与空弦振动频率完全相等呢？这就需要“共鸣原理”：当两种振动的频率相等时合成的效果得到最大的加强而没有丝毫的减弱。因此你应当通过体验与感悟去调整你的声带振动频率使声带振动与空弦振动发生共鸣，此时声带振动频率等于空弦振动频率。
二.绝对音高
从历史上看，绝对音高一直都在变化，不同国度、不同地区、不同地区、不同时代都有不同的标准，根据对欧洲保留下来的管风琴所做的测定，中央C上方A（即我们熟知的la）的频率范围为377-567HZ，从19世纪开始，在欧洲和北美音乐实践中，人们趋向于不断地提高绝对音高（A的频率），这个现象的背后有着技术进步的原因：首先，材料科学的进步使得人们能够制作出更细同时又经受得起更大张力的琴弦；其次，制作技术的进步也使传统乐器能够发出更高的声音，还有乐器制作者之间的竞争也不断推动绝对音高的提升。另外，随着建筑技术的进步，音乐厅的规模越来越大，能够容纳的听众越来越多，而提升绝对音高可以使得乐队的声音效果显得更加嘹亮和华丽。
然而，人的嗓音是不可能无限制地提高的，歌唱家是提升绝对音高的坚定反对者，数学家Harold Coxeter曾经这样写道：“贝多芬时代的标准音高大概是$426\frac{2}{3}$，但是，今天的音乐会音高(concert pitch)不是427，而是A=440，这就使得女高音陷入悲惨的境地，当别的声部都在歌颂欢乐的时候，女高音们却要连续在12小节中保持高音A”。
为了解决这个问题，在一些地方，政府或者行业协会出面制定了区域性的绝对音高标准。例如，1834年召开的斯图加特(Stuttgard)会议推荐以$C_4$=264HZ作为标准音高，按照纯律计算，相当于$A_4$=440HZ。1895年2月，法国政府通过法律，确定$A_4$=435HZ，1896年，伦敦皇家爱乐协会(Royal Philharmonic Society)确定$A_4$=439HZ。
进入20世纪之后，随着广播、录音等产业的发展，日益需要制定一个国际通行的绝对音高标准。1939年5月国际标准化协会(ISA)在伦敦召开会议，正式确立$A_4$=440HZ为音乐会音高，1955年，国际标准化组织(International Organization for Standardization, IOS)把$A_4$=440HZ座位技术标准，此后一直沿用至今。
Q1:为什么钢琴的do是do呢？
A1:1955年，国际标准化组织(International Organization for Standardization, IOS)把$A_4$=440HZ座位技术标准，此后一直沿用至今。
三.相对音高
了解了绝对音高之后，我们接下来了解相对音高，即音和音之间的区别和联系。精确度量音程的单位是音分(cents)，它是英国数学家亚历山大·埃利斯提出的。音分是度量不同声音的频率比的单位。设两个声音的频率分别为$f_1,f_2$，且$f_1<f_2$，频率比 $r=f_2/f_1$
，那么这两个声音之间的音分$c$定义为$$c=1200log_2r=1200log_2\frac{f_2}{f_1}$$
以下是四种调律的音分
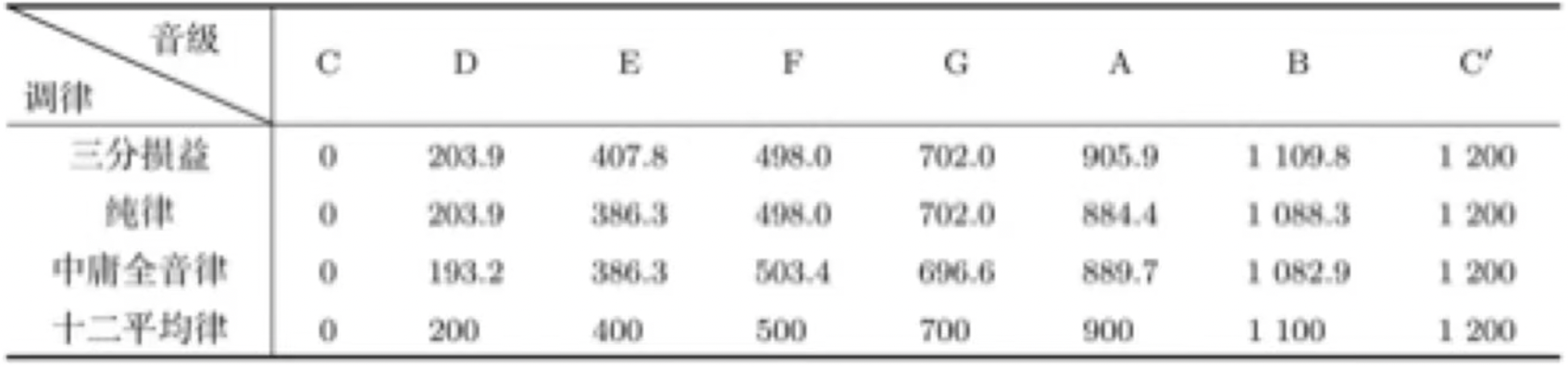音分的定义主要基于现代广泛应用的十二平分律，故对于十二平分律其音分简单明确，对于其他音律，虽然有些许出入但整体偏差不大，也体现出从古至今音律学者们对音乐的整体追求是相同的。
了解了绝对音高及相对音高的衡量方法后，下面我们进入重头戏–根据音的频率来介绍一下不同调律。
四.调律
梅森定律说明弦的振动频率（音高）与其长度成反比，与其张力的平方成正比，而与弦的线密度的平方根成反比。进一步，$u(x,t)$是通项$u_n(x,t)$的无穷级数，这说明弦的震动并非简单的单一频率运动，而是无数个正弦震动的叠加 $u_n(x,t) (n=1,2,3,…)$ 称为弦振动的第n个振动模态(mode of vibration)，其振动频率为 $$f_n=\frac{n}{2L}c=\frac{n}{2L}\sqrt{\frac{T}{\rho}}\quad n=1,2,3,…$$ 序列${f_1,f_2,f_3,…}$称为弦的固有频率(natural frequencies)，$f_1$称为基频(fundamental frequency)，而${f_2,f_3,f_4,…}$所对应的声音统称为泛音(overtone)。更准确地说，$f_2$对应的是第一泛音，$f_3$对应的是第二泛音，以此类推，可以看出，泛音的频率都是基频的整数倍。设基频为$f$，则固有频率序列为：$$f,2f,3f,4f,5f,…$$ 音乐上通常把这个序列称为泛音列。
有了泛音列的概念，就可以介绍赫尔姆霍兹对于音程是否和谐的另一个解释：泛音列重合理论，假设两个乐音的基频分别是$f_1$和$f_2$，那么这两个乐音其实包含了各自的泛音列。 $$f_1,2f_1,3f_1,4f_1,…$$ $$f_2,2f_2,3f_2,4f_2,…$$ 当第二个乐音比第一个乐音高八度时，其弦长度为第一个乐音的$\frac{1}{2}$，根据梅森定律，其振动频率是第一个乐音的2倍，故其基频$f_2=2f_1$，代入第二个乐音的泛音列： $$f_1,2f_1,3f_1,4f_1,…$$ $$2f_1,4f_1,6f_1,8f_1,…$$ 不难看出，这些泛音在第一个乐音的泛音列中都有出现，即第二个泛音列是第一个泛音列的子列，在音乐效果上，这两个乐音构成的音程是完全协和的。
Q2：为什么有音高的循环呢，C和高八度的C有什么关系？
A2：每个音都可分解为由一次谐波与一系列整数倍频率谐波的叠加。而两个音的两列谐波的频率几乎相同时，会产生近似于共鸣的效果。由此可推出一个原理：两音的频率比若是简单的整数关系则两音具有和谐的关系，因为每个音都可分解为由一次谐波与一系列整数倍谐波的叠加，两音的频率比愈是简单的整数关系意味着对应的两个谐波列含有相同频率的谐波愈多，例如一对八度音则是1:2的频率比。 do和高八度的do,re和高八度的re，都是上文中提到$f_1$和$f_2$的关系，高八度的do是do弦长的一半，频率是do的二倍，泛音列是do的子列，所以理论上大字组小字组所有的do同时弹奏时都是最和谐的。
我们用不同的音组合成曲调，当然要考虑这些音放在一起是不是很和谐，前面已谈到八度音是在听觉和谐效果上关系最密切的音，但是仅用八度音不能构成动听的曲调——至少它们太少了，例如在音乐频率范围内 c1 与 c1 的八度音只有如下的 8 个：C2（16.35赫兹）、C1（32.7赫兹）、C（65.4赫兹）、c（130.8赫兹）、c1（261.6赫兹）、c2（523.2赫兹）、c3（1046.4赫兹）、c4（2092.8赫兹），对于人声就只有C、c、c1、c2这4个音了。
为了产生新的和谐音，不同的调律被发明出来丰富音乐的音高。
4.1 毕达哥拉斯五度相生律
回顾一下前面说的一对八度音和谐的原理是近似于共鸣，因为泛音的频率都是基频的整数倍，所以频率比是1:2的两个音之间可以产生和谐的共鸣，利用相同的思路，其他整数比例也可以产生相似的效果，例如3:2。
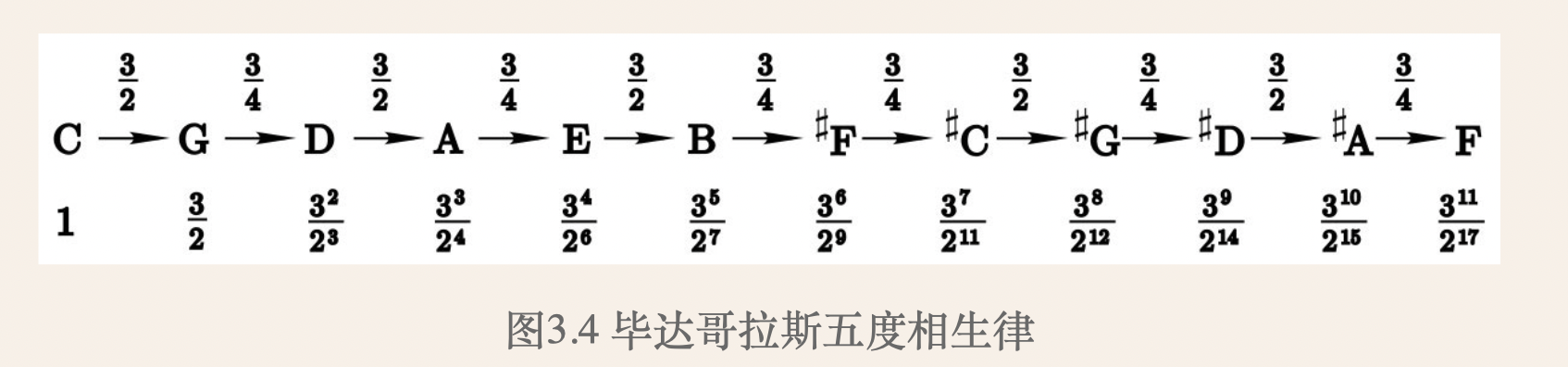
假定音级C对应的频率为f，则其上方五度G对应的频率为($\frac{3}{2}f$)，而G再上方五度音的频率应该是($(\frac{3}{2})^2f$)>2f，超出了同一个八度，因此将其降低一个八度，得到音级D对应的频率为($\frac{9}{8}f$)，然后继续上面的做法，每次用$\frac{3}{2}$去乘，如果得到的数大于2超出了同一个八度，就再多乘一个$\frac{1}{2}$，直到产生全部7个音级，这个过程的通项式为$$P_n=\frac{(3/2)^n}{2^{(nlog_2{\frac{3}{2}})}}$$
| $P_n$ | $\frac{2}{3}^n$ | $\frac{(3/2)^n}{2^{(nlog_2{\frac{3}{2}})}}$ | 音列 | 音级 |
|---|---|---|---|---|
| $P_0$ | 1 | 1 | 1 | C |
| $P_1$ | 1.5 | $\frac{3}{2}$ | 1.5 | G |
| $P_2$ | 2.25 | $\frac{9}{8}$ | 1.125 | D |
| $P_3$ | 3.375 | $\frac{27}{16}$ | 1.6875 | A |
| $P_4$ | 5.0625 | $\frac{81}{64}$ | 1.265625 | E |
| $P_5$ | 7.59375 | $\frac{243}{128}$ | 1.8984375 | B |
| $P_6$ | 11.390625 | $\frac{729}{512}$ | 1.423828125 | F |
可以看到这是一个循环音列，音列P(k)和后继音级P(k+1)之间都包含5个音级——它们之间的度数是五，这就是“五度相生律”名字的由来。
拓展阅读：毕达哥拉斯音差(Pythagorean comma) 。
如果从 C 开始依次用频率比 3∶2 制出新的音，在某一次新的音恰好是 C 的高若干个八度音，那么再往后就不会产生新的音了。很可惜，数学可以证明这是不可能的，因为没有自然数m、n会使下式成立： $$(3/2)^m=2^n$$ 所以这必然是一个螺旋无终点的过程，用数学表示即F上方五度是高八度的C‘，降低八度得到的应该就是起始音级C。换言之$\frac{3^{12}}{2^{19}}=\frac{5314441}{524288}\approx1.013643$应该等于1才对，这个略大于1的数就是毕达哥拉斯音差。
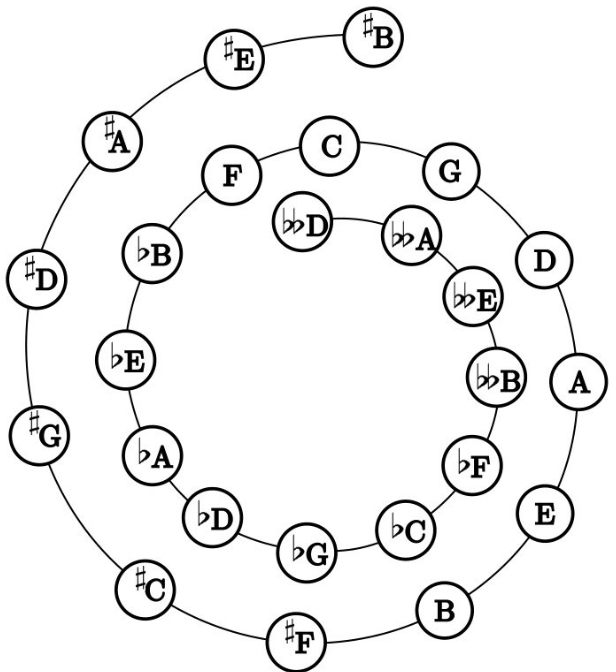
再具体细看此现象对每个音级之间的比例的影响，纯五度音程的频率比无疑都是3:2，纯四度音程频率比也是相等的，都是4:3，例如D-G的频率比为$\frac{3}{2}:\frac{3^2}{2^3}=\frac{4}{3}$。但是，看三度和六度音程就会发现问题：音程C-E的频率比为$\frac{3^4}{2^6}:1=\frac{81}{64}=1.265625$大于完美的大三度比例5:4。 而大六度音层C-A，D-B的频率比都是$\frac{27}{16}=1.6875$，大于完美的比例5:3。
在早期的西方音乐中，纯四度和纯五度音程所起的作用远比三度和六度音程更加重要。所以，五度相生法产生的音乐体系首先保证了最主要的音程和谐动听，而对次要音程就只能有所牺牲了。
4.2 纯律
从文艺复兴时期开始，西方音乐中越来越多地重视和使用三度和六度音程，于是人们探索在五度相生法中添加一个生律元素：理想大三度的比例5:4，形成了纯律(just intonation)。
仍然假定音级C对应频率1。因为八度音程的频率比为2:1，而一个四度音程与一个五度音程(3/2)合起来就得到一个八度音程，所以四度音程的频率比应为：$$2\div \frac{3}{2}=4:3$$
从而得到音级F对应的频率为$\frac{4}{3}$，再由大三度音程F-A得到音级A对应的频率应该等于F的频率乘以新加入的大三度生律元素5:4，即得：$$\frac{4}{3}\times\frac{5}{4}=\frac{5}{3}$$
由纯五度E-B得到关系式$x:\frac{5}{4}=3:2$，求得音级B的频率x为$\frac{15}{8}$，这时大三度音程G-B、纯四度音程B-E‘等也都满足理想的频率比。
最后来确定D的频率，假定其高八度音级D’对应的频率为y，由纯五度音程G-D’得到关系式$y:\frac{3}{2}=3:2$，进而得到D的频率为$\frac{9}{4}$。这样我们就得到纯律各音级的相对频率如下图：
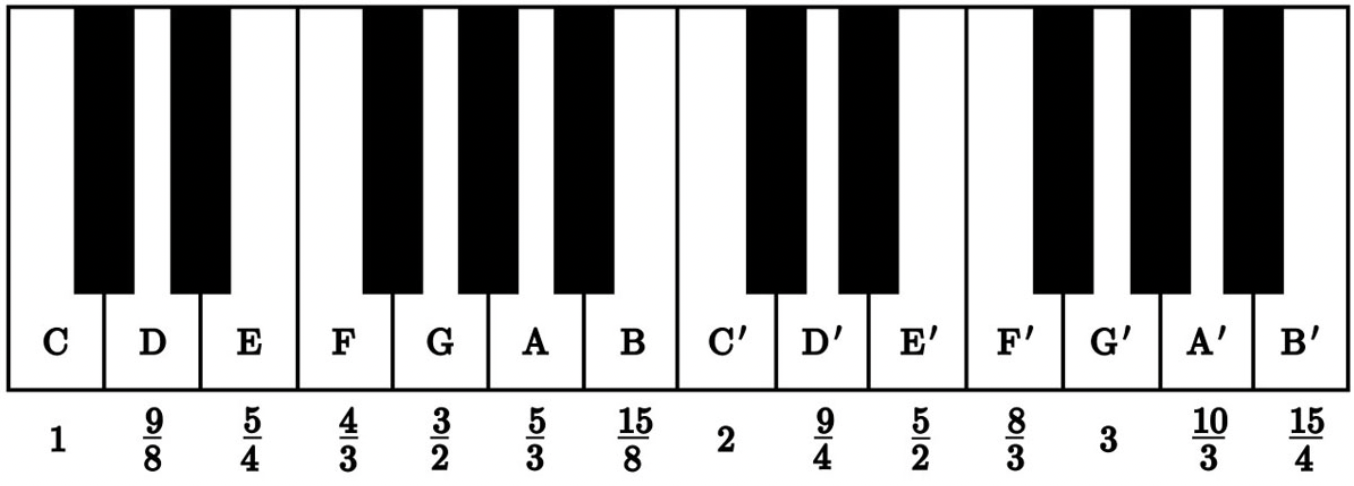
纯律的优点在于：大三和弦C-E-G，F-A-C'，G-B-D’的频率比都符合理想的4:5:6，比五度相生律中的大三和弦更加悦耳，这在复调音乐(polyphony)中尤为重要。
下表格展示了五度相生律和纯律的相似点和差别。
| 音级 | 五度相生律 | 五度相生律 | 纯律 | 纯律 |
|---|---|---|---|---|
| C | 1 | 1 | 1 | 1 |
| D | $\frac{9}{8}$ | 1.125 | $\frac{9}{8}$ | 1.125 |
| E | $\frac{81}{64}$ | 1.265625 | $\frac{80}{64}$ | 1.25 |
| F | $\frac{729}{512}$ | 1.423828125 | $\frac{4}{3}$ | 1.333 |
| G | $\frac{3}{2}$ | 1.5 | $\frac{3}{2}$ | 1.5 |
| A | $\frac{27}{16}$ | 1.6875 | $\frac{5}{3}$ | 1.667 |
| B | $\frac{243}{128}$ | 1.8984375 | $\frac{15}{8}$ | 1.875 |
但是纯律也有明显的缺点，第一个缺点是五度音程D-A不和谐，其频率比为$\frac{5}{3}:\frac{9}{8}=\frac{40}{27}=\frac{80}{54}$不等于理想的$3:2=81/54$，两者之差$$\frac{81}{54}:\frac{80}{54}=\frac{81}{80}=1.10125$$ 称之为谐调音差(syntonic comma)。
纯律的第二个缺点是有两种不同的大二度（全音）：音程C-D，F-G，A-B的频率比均为9/8，而音程D-E，G-A的频率比均为10/9。
最后一个缺点，同五度相生法一样，由于$$(3/2)^m=2^n$$是无解的，纯律也是无法通过持续计算，经过n次后，回到高m个八度的C音的，蔡元定所说的“三分损益之数往而不返”是完全正确的，这就导致音程的频率比五法统一，也就导致了转调困难。
将调式中的其他音级作为主音来生成音级，这叫做转调。由于邻音的音程不同，转调十分困难。在对数尺上“比例关系”变为“距离关系”，转调即是其上的平移。因为半音的问题，平移主音之后整个音列无法与原先的音列对齐。例如，取二音为主音按照五度相生律计算，它的下属音就不在以一音为主音的调式中。
4.3 十二平均律
要解决转调和音程的频率比不统一的问题，最终都归结为如何把音差尽可能平均分配给一个八度中不同音级之间形成的各个音程。例如，南朝宋人何承天所发明的“新律”，就是把三分损益法产生的音差平分为12份，然后把这个平均数累加到十二律上，使得十二律在音差部分形成一个等差数列。但是，正如我们已经指出的，音程关系是相乘而非相加，用等差数列是不能解决根本问题的，我们需要的是等比数列！
现在问题就非常简单了，我们只需要在C(1)和C'(2)之间，插入11个音，使这13个音呈现以1开头，以2结尾的等比数列就可以了，即公比为$\sqrt[12]{2}$。 世界上第一个明确提出平均律，并且精确计算出公比$r=\sqrt[12]{2}$的是中国明代的朱载堉，他创建平均律理论的代表作有《律吕精义》、《律学新说》和《算学新说》等。朱载堉将其创建的平均律称作“新法密率”，为了解决旋宫不归的问题，经过常年的研究琢磨，朱载堉提出了：“不用三分损益之法，创立新法。置一尺为实，以密率除之，凡十二遍，所求率吕真数，比古四种术尤简洁而精密”，这里的“密率”就是朱载堉在世界上首次通过勾股术计算出来的、具有25位精确度的$\sqrt[12]{2}$。
另外，在西方文献中首次出现十二平分律的公比$\sqrt[12]{2}\approx 1.059463$的是1636年出版的梅森的《和声学通论》(Harmonie Universelle)。 赫尔姆霍茨曾经写道：“中国有一位王子名叫载堉，力排众议，创导七声音阶。而将八度分成12个半音的方法，也是这个富有天才和智巧的国家发明的。”。英国科学技术史专家李约瑟指出：朱载堉对人类的贡献是发现了以相等的音程来调音阶的数学方法。首先给出平均律数学公式的荣誉无疑应当归之于中国。
这看起来非常简单，但是是音乐和数学届的一大步，因为$\sqrt[12]{2}$是一个无理数，无理数是数学中一大怪物，当今一个非数学专业的大学生在学完大学数学之后仍然不明白无理数是什么，数学家使用无理数已有2500多年也直到19世纪末才真正认识无理数。音乐家似乎不在乎无理数的艰深，轻易地将高雅音乐贴上了无理数的标签。
十二平均律的出现还使得我们在前面推出的和谐性原理——两音的频率比愈是简单的整数关系则两音愈具有和谐的关系——不再成立。不过不必为此而沮丧，因为本质上说艺术行为不是一定要服从科学道理的。正如符合黄金分割原理的绘画是艺术，反其道而行之的绘画也是艺术。
| 均分 | 十二平均律 | 音级 | 五度相生律 | 五度相生律 | 纯律 | 纯律 |
|---|---|---|---|---|---|---|
| 0 | 1 | C | 1 | 1 | 1 | 1 |
| $\frac{1}{2}$ | 1.059463094 | |||||
| 1 | 1.22462048 | D | $\frac{9}{8}$ | 1.125 | $\frac{9}{8}$ | 1.125 |
| $1\frac{1}{2}$ | 1.189207115 | |||||
| 2 | 1.25992105 | E | $\frac{81}{64}$ | 1.265625 | $\frac{80}{64}$ | 1.25 |
| $2\frac{1}{2}$ | 1.334839854 | |||||
| 3 | 1.414213562 | F | $\frac{729}{512}$ | 1.423828125 | $\frac{4}{3}$ | 1.333 |
| $3\frac{1}{2}$ | 1.498307077 | G | $\frac{3}{2}$ | 1.5 | $\frac{3}{2}$ | 1.5 |
| 4 | 1.587401052 | |||||
| $4\frac{1}{2}$ | 1.681792831 | A | $\frac{27}{16}$ | 1.6875 | $\frac{5}{3}$ | 1.667 |
| 5 | 1.781797436 | |||||
| $5\frac{1}{2}$ | 1.88 | B | $\frac{243}{128}$ | 1.8984375 | $\frac{15}{8}$ | 1.875 |
| 6 | 2 | C‘ | 2 | 2 | 2 | 2 |
Q3：为什么钢琴是3个黑键-4个黑键一组，而不是2个黑键-5个黑键一组？B-C间、E和F间是自然半音，而其他C和D、D和E等之间都是自然全音呢？
A3：从上表我们可以看到，五度相生律计算出来的七个音排列，四五、七八之间的比（半音音程）小于其他相邻音之间的比（全音音程），导致了一个七声调式中的音阶里一定会出现两个半音音程；后来，又选取了现在所说的“大调调式”，将半音音程“移动”到了三四、七八音之间，稳定了下属音（4）到主音（1）、主音到属音（5）之间的五度关系，使之都是纯五度。钢琴也是基于这种大调调式。
Q4：音高是连续的，人类以什么样的标准制造音阶以获得和谐好听的音乐？
A4：通过生律方法生出来的音阶有很多，例如五度相生律可以无限制得生成音阶出来，但是我们没有必要把所有生出的音都拿去构建音阶，否则在通行西洋音乐体系下，我们就只有半音阶这一种音阶了。 音阶（在这里包含 mode）的构造，是在生律完成后，选择一些音去构成一个音高依次递增的序列。具体如何选择，则有很多种可能性。最显而易见的，是我们经常使用三种小调。升 F 代替 F 的调式是 Lydian 调式。在中国古代音乐中，在五音的基础上加上升 F 和 B 就形成了雅乐调式。 使用较为广泛的大调音阶（全全半全全全半）的构造，并不是以生音顺序为准则的。大调式的构成逻辑是，是以作为大三和弦的主三和弦、属三和弦和下属三和弦为骨架去构造音阶。主三和弦：C E G；属三和弦：G B D；下属三和弦：F A C。把这些音都放到一个八度内，去除重复音，按音高排序，就得到了大调式。以这些骨架和弦为基础、逐渐吸纳无他和弦构建出的和声理论，就是功能和声。
音乐理论是从长期、大量的音乐实践活动中总结出来的，倘若忽视了历史发展，就不免有“穿凿附会”之嫌。当音乐发展到一定阶段，对丰满、成熟的体系做纯粹理性分析，提出新的观点、建立新的认知，符合结构主义做派。但从本质上说艺术行为不是一定要服从科学道理的。正如符合黄金分割原理的绘画是艺术，反其道而行之的绘画也是艺术。
参考资料：
[1]王杰. 音乐与数学[M]. Beijing da xue chu ban she, 2019.
[2]黄力民，音乐中的数学，三思科学电子杂志
[3]音的三种律法：发展与联系，知乎
[4]李重光. 音乐理论基础[J]. (No Title), 1962.