推荐系统的终极优化目标应包括两个维度：一个维度是用户体验的优化，另一个维度是满足公司的商业利益。对一个健康的商业模式来说，这两个维度应该是和谐统一的。例如YouTube的用户体验和公司利益（时长越长广告曝光越多）在“观看时长”这一点上达成了一致。

下图是推荐系统的技术架构示意图。其中数据部分为融合了数据离线批处理、实时流处理的数据流框架；算法和模型部分则为集训练(training)、评估(evaluation)、部署(deployment)、线上推断(online inference)为一体的模型框架。

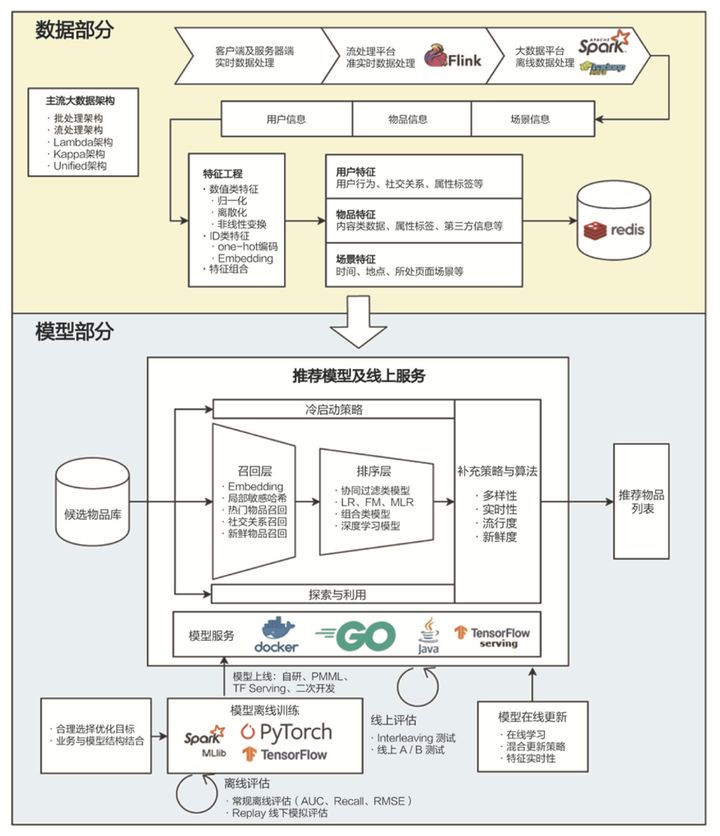
推荐系统的进化之路

传统推荐模型

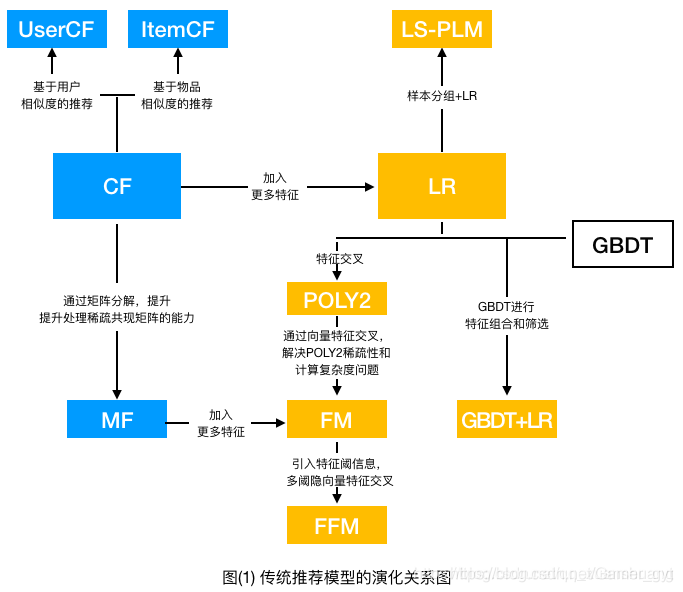
一. 协同过滤算法

UserCF基于用户相似度进行推荐，它符合人们直觉上的“兴趣相似的朋友喜欢的物品，我也喜欢”的思想，这使其具有更强的社交属性，这样的特点使其非常适合新闻推荐场景，因为新闻本身的兴趣点往往是分散的，相比用户对不同兴趣的偏好，新闻的及时性、热点性往往是其更重要的属性，而UserCF正适用于发现热点，以及跟踪热点的趋势。而ItemCF适用于兴趣变化较稳定的应用，例如Amazon、Youtube等。但从技术角度，它主要有两个缺点，首先是，互联网应用场景下，用户数往往远大于物品数，而UserCF需要维护用户相似度矩阵以便快速找出$Top n$相似用户，这使得存储开销非常大$O(n^2)$，第二点是用户的历史数据向量非常稀疏，对于只有几次购买或点击的用户来说，找到相似用户的准确度是非常低的，这导致UserCF不适用于哪些正反馈获取困难的场景（如酒店预订、大件商品购买等低频应用）。

ItemCF解决了上述存储开销大的问题，但是由于数据稀疏，它仍然有协同过滤的天然缺陷——推荐结果的头部效应较明显，处理稀疏向量的能力弱。为了增强模型的泛化能力，矩阵分解技术被提出。相比协同过滤，矩阵分解的①泛化能力强，可以在一定程度上解决数据稀疏问题，②空间复杂度低，只需存储用户和物品隐向量，空间复杂度由$O(n^2)$降低到$O((m+n)\cdot k)$级别。③具有更好的扩展性和灵活性，这其实与Embedding思想不谋而合，因此矩阵分解的结果也非常方便与其他特征进行组合和拼接，并便于与深度学习网络进行无缝结合。

与此同时，矩阵分解也有一定局限性。它不方便加入其他特征，丧失了利用很多有效信息的机会。为了解决这个问题，逻辑回归及其后续发展出的因子分解机等模型，凭借其天然的融合不同特征的能力，逐渐在推荐系统领域得到更广泛的应用。

1.UserCF

共现矩阵中，和你评分行为相似的TopN用户对物品p的评分。其中值得注意的两部分为 ①用户相似度和②最终结果排序

①理论上，任何合理的“向量相似度定义方式”都可以作为相似用户计算的标准。例如余弦相似度，皮尔森相关系数，相比余弦相似度减小了用户评分偏置的影响。

②最常用的方式是利用用户相似度和相似用户的评价的加权平均获得目标用户的评价预测

$R^(u,p)=\cfrac{\sum_{s\in{S}}(W_{u,s}\cdot{R_{s,p}})}{\sum_{s\in{S}}W_{u,s}}$

其中，权重$W_{u,s}$是用户$u$和用户$s$的相似度，$R_{s,p}$是用户$s$对物品$p$的评分。

2.ItemCF

利用物品相似度矩阵，针对目标用户历史行为中的正反馈物品，找出相似的$Topk$物品，对这些物品进行相似度分值排序，相似度分值为与已有正反馈物品相似度的累加。

$R_{u,p} = \sum_{h\in{H}}(W_{p,h} \cdot R_{u,h})$

其中，$H$是目标用户的正反馈物品合集，$w_{p,h}$是物品$p$与物品$h$的物品相似度，$R_{u,h}$是用户$u$对物品$h$的已有评分。

3.矩阵分解

该方法在协同过滤共现矩阵的基础上，使用更稠密的隐向量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征，在一定程度上弥补了协同过滤模型处理稀疏矩阵能力不足的问题。但仍无法引入用户画像信息、物品画像信息和实时上下文信息，这就需要机器学习模型来解决了。

矩阵分解算法将$m \times n$维的共现矩阵R分解为$m \times k$维的用户矩阵$U$和$k \times n$维的物品矩阵$V$相乘的形式。其中$k$是隐向量的维度，$k$的大小决定了隐向量表达能力的强弱。$k$的取值越小，隐向量包含的信息越少，模型的泛化程度越高；反之，$k$的取值越大，隐向量的表达能力越强。在具体应用中，$k$的取值要经过多次试验找到一个推荐效果和工程开销的平衡点。

矩阵分解主要有三种方法：①特征值分解(Eigen Decomposition)、奇异值分解(Singular Value Decomposition, SVD)和梯度下降(Gradient Descent)。其中特征值分解只能作用于方阵，显然用户-物品矩阵不是。奇异值分解存在两点缺陷，使其不宜作为互联网场景下矩阵分解的主要方法：①奇异值分解要求共现矩阵是稠密的，如果要应用，就要对缺失元素进行填充。②传统奇异值分解的计算复杂度达到了$O(mn^2)$，这对于动辄上千万的互联网场景来说不可接受。

由上，梯度下降成了进行矩阵分解的主要方法，加入正则化项的目标函数入下：

$\underset {q^,p^}{min}\underset {(u,i)\in K}{\sum}(r_{ui}-q_i^Tp_u)^2+\lambda(||q_i||+||p_u||)^2$

隐向量的生成过程其实是对共现矩阵进行全局拟合的过程，因此隐向量其实是利用全局信息生成的，有更强的泛化能力；而协同过滤中只利用用户和物品自己的信息进行相似度计算，这就使协同过滤不具备泛化利用全局信息的能力。

为了消除用户和物品打分的偏差(Bias)，常用的做法是在矩阵分解时加入用户和物品的偏差向量：

$r_{ui} = \mu + b_i + b_u +q_i^Tp_u$

其中$\mu$是全局偏差常数，$b_i$是物品偏差系数，可使用物品$i$收到的所有评分的均值，$b_u$是用户偏差系数，可使用用户$u$给出的所有评分的均值。与此同时，目标函数也要有相应改变：

$\underset {q^,p^,b_*}{min}\underset {(u,i)\in K}{\sum}(r_{ui}- \mu -b_u-b_i-q_i^Tp_u)^2+\lambda(||q_i||+||p_u||+b_u^2+b_i^2)^2$

二.逻辑回归

逻辑回归作为广义线性模型的一种，使用softmax(二分类退化为sigmoid)映射线性模型至0-1，符合点击率的物理性质。目标函数可以分别通过交叉熵和服从伯努利的最大似然推导（最大似然取log后与交叉熵损失函数等价），参数训练常采用的方法为梯度下降法、牛顿法、拟牛顿法等。

逻辑回归的优点在于，①数学含以上的支撑，点击率这个行为服从伯努利分布的这个假设，采用逻辑回归作为CTR模型是符合“点击”这一事件的物理意义的。②权重可解释性强。③易于并行化、模型简单、训练开销小。

但它也有局限性，它表达能力不强，无法进行特征交叉、特征筛选等一系列较为“高级”的操作，因此不可避免地造成信息的损失。为了解决这一问题，衍生出因子分解机等高维的复杂模型，在进入深度学习时代后，多层神经网络强大的表达能力可以完全替代逻辑回归模型。

三.从FM到FMM-自动特征交叉的解决方案

算法工程师手动组合特征，再通过各种分析手段筛选特征的，这种方法无疑是低效的，并且人类的经验往往有局限性，程序员的精力和时间无法支撑找到最优的特征组合。于是，模型自动特征交叉的方案应运而生。

1.POLY2模型——特征交叉的开始

$\phi POLY2(w,x)=\sum^n_{j_1 = 1} \sum^n_{j_2 = j_1+1}w_h(j_1,j_2)x_{j_1}x_{j_2}$

该模型对所有特征两两交叉(特征$x_{j_1}$和$x_{j_2}$)，并对所有的特征组合赋予权重$w_{h(j_1,j_2)}$。POLY2通过暴力组合特征的方式，在一定程度上解决了特征组合的问题。POLY2模型本质上仍是线性模型，训练方法与逻辑回归并无区别，因此便于工程上的兼容。但是PLOY2模型存在两大缺陷，①one-hot编码的稀疏特征，交叉后更加稀疏，导致大部分交叉特征的权重缺乏有效数据训练，无法收敛。②权重参数的数量由$n$直接上升到$n^2$，极大地增加了训练的复杂度。

2.FM模型——隐向量特征交叉

与POLY2不同的是，FM用两个向量的内积$(w_{j_1} \cdot w_{j_2})$取代了单一的权重系数$w_h(j_1,j_2)$。具体地说，FM为每个特征学习了一个隐权重向量(latend vector)。在特征交叉时，使用两个隐向量的内积作为权重，这和矩阵分解的隐向量有着异曲同工之妙：

$\phi FM(w,x)=\sum^n_{j_1 = 1} \sum^n_{j_2 = j_1+1}(w_{j_1} \cdot w_{j_2})x_{j_1}x_{j_2}$

此时参数数量为$nk$（$k$为隐向量维度，$n»k$），使用梯度下降法进行训练时复杂度可被同样降低到$nk$级别，极大降低了训练开销。

同时，隐向量更好地解决了数据稀疏性问题。POLY2中只有两种特征取值同时出现时，才能学习这个组合的权重，例如(‘male’,‘earrings’)，当这两种特征出现次数非常少时，则此参数缺乏有效训练。而隐向量可以通过(‘male’,xx)和(xx,‘earrings’)分别训练隐向量。这样，甚至对于一个从未出现过的组合，由于模型之前已经学习过两个的分别隐向量，也具备了计算该特征组合权重的能力。所以，相比POLY2，FM虽然丢失了某些具体特征组合的精确记忆，但是泛化能力大大提高。

在工程方面，FM同样可以使用地图下降法，使其不失实时性和灵活性。相比之后深度学习复杂的网络结构导致难以部署和线上服务。FM较容易实现的模型结构使其线上推断的过程相对简单，也更容易进行线上部署和服务。因此，FM在2021-2014年前后，成为业界主流的推荐模型之一。

3.FFM模型——引入特征域的概念

相比FM模型，FMM模型引入了特征域感知(field-aware)这一概念，使模型的表达力更强。

$\phi FMM(w,x)=\sum^n_{j_1 = 1} \sum^n_{j_2 = j_1+1}(w_{j_1,f_2} \cdot w_{j_2,f_1})x_{j_1}x_{j_2}$

当$x_{j1}$特征与$x_{j2}$特征进行交叉时，$x_{j1}$特征会从$x_{j1}$的这一组隐向量中挑出与特征$x_{j2}$的域$f_2$对应的隐向量$w_{j1,f_2}$进行交叉。这里说的 域(field)是指某个分类特征one-hot形成的一段特征向量。

FMM保留了域的概念增强了模型表达能力，这也导致计算复杂度上升到$kn^2$，在实际工程应用中，需要在模型效果和工程投入之间进行权衡。

四.GBDT+LR——特征工程模型化的开端

无论是FM还是FMM都是在做二阶特征交叉，如果继续提高特征交叉维度，会不可避免地产生组合爆炸和计算复杂度过高的问题。2014年，Facebook提出了基于GBDT+LR的组合模型解决方案。利用GBDT自动进行特征筛选和组合，进而生成新的离散特征向量，再把该特征向量当作LR模型输入。GBDT和LR这两步是独立训练的，所以不存在如何将LR的梯度回传到GBDT这类复杂问题。

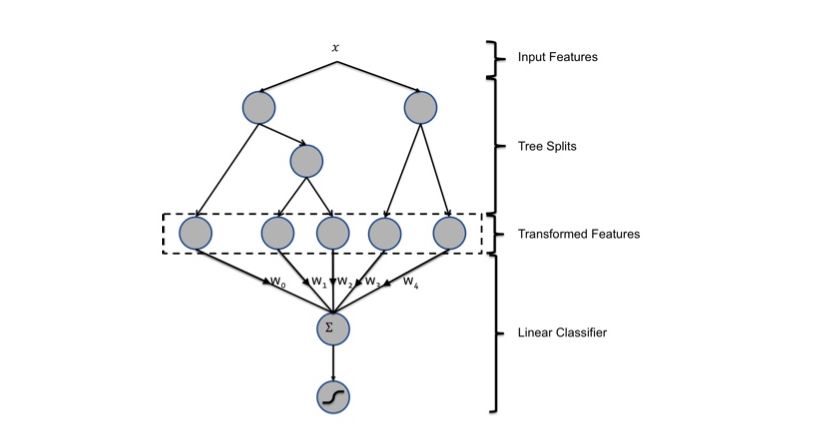
GDBT是由多棵回归树组成的树林，后一棵树以前面树林的结果与真实结果的残差为拟合目标。每棵树生成的过程是一棵标准的回归树生成过程，因此书中每个节点的分裂是一个自然的特征选择过程，而多层节点的结构则对特征进行了有效的自动组合，GDBT中每一个树都是一个交叉特征，而树的深度决定了交叉的阶数。

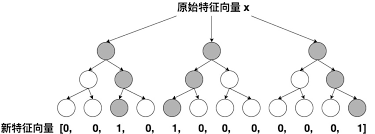
虽然GDBT有如此强大的特征组合能力，但GBDT容易产生过拟合，以及丢失了大量特征的数值信息，因此不能直接说GBDT的交叉能力强，效果就比FMM好，在模型的选择和调试上，永远都是多种因素综合作用的结果。

五.LS-PLM——阿里巴巴曾经的主流推荐模型

LS-PLM(Large Scale Piece-wise Linear Model,大规模分段线性模型)虽然在2017年才被阿里巴巴公之于众，但其实早在2012年，它就是阿里巴巴主流的推荐模型，并在深度学习模型提出之前长时间应用于阿里巴巴的各类广告场景。LS-PLM的结构与三层神经网络极其相似，在深度学习来临的前夜，可以将它看作推荐系统领域连接两个时代的节点。

LS-PLM，又被称为MLR(Mixed Logistic Regression，混合逻辑回归)，它在逻辑回归的基础上采用分而治之的思想，先对样本分片，再在样本分片中引用逻辑回归进行预估，其灵感来自对广告推荐领域样本特点的观察。为了让CTR模型对不同用户群体、不同使用场景更有针对性，其采用的方法是先对全量样本进行聚类，再对每个分类施以逻辑回归模型进行CTR预估。

$f(x)= \sum ^m _{i=1} \pi_i(x) \cdot \eta_i(x) = \sum ^m {i=1} \cfrac {e^{\mu_i \cdot x}}{\sum^m{j=1} e^{\mu_j \cdot x}} \cdot \cfrac {1}{1+e^{-w_i \cdot x}} $

先用聚类函数$\pi$对样本进行分类(这里的$\pi$采用了$softmax$函数对样本进行多分类)，这个样本对每个分类都有一个概率值，这些值的和为1($softmax$的性质)。再用LR模型计算每个切片（类）的CTR，然后求加权CTR和。其中的超参数“分片数”m可以较好地平衡模型，当m=1时，LS-PLM就退化为普通LR模型，m越大，模型的拟合能力越强。但与此同时，模型参数规模也随m的增长而线性增长，模型收敛所需的训练样本也随之增长。在实践中，阿里巴巴给出的m的经验值为12.

LS-PLM模型适用于工业级的推荐、广告等大规模稀疏数据的场景，主要是有以下两个优势①端到端的非线性学习能力②模型的稀疏性强（L1范数比L2范数更容易产生稀疏解），部署更加轻量级。

从深度学习角度重新审视LS-PLM模型，LS-PLM模型可以看作一个加入了注意力(Attention)机制的三层神经网络模型，其中输入层是样本的特征向量，中间层是由m个神经元组成的隐层，其中m是分片的个数，对于一个CTR预估模型，LS-PLM的最后一层自然是由单一神经元组成的输出层。那么，注意力机制又是哪里应用的呢？其实是在隐层和输出层之间，神经元之间的权重是由分片函数得出的注意力得分来确定的，也就是说，样本属于哪个分片的概率就是其注意力得分。

传统推荐模型总结

模型名称	基本原理	特点	局限性
协同过滤	根据用户的行为历史生成用户-物品共现矩阵，利用用户相似性和物品相似性进行推荐	原理简单、直接，应用广泛	泛化能力差，处理稀疏矩阵的能力差，推荐结果的头部效应明显
矩阵分解	将协同过滤算法中的共现矩阵分解为用户矩阵和物品矩阵，利用用户隐向量和物品隐向量的内积进行排序并推荐	相较协同过滤，泛化能力有所增强，对稀疏矩阵的处理能力有所增强	除了用户历史行为数据，难以利用 其他用户、物品特征及上下文特征
逻辑回归	将推荐问题转换成类似CTR预估的二分类问题，将用户、物品、上下文等不同特征转换成特征向量，再按照预估CTR进行排序并推荐	能够融合多种类型的不同特征	模型不具备特征组合能力，表达能力较差
FM	再逻辑回归的基础上，再模型中假如二阶特征交叉部分，为每一维特征训练得到相应特征隐向量，通过隐向量的内积运算得到交叉特征权重	相比逻辑回归，具备了二阶特征交叉能力，模型的表达能力有所增强	由于组合爆炸问题的限制，模型不易扩展到三阶特征交叉阶段
FFM	在FM模型的基础上，加入“特征域”的概念，使每个特征在与不同域的特征交叉时采用不同的隐向量	相比FM，进一步加强了特征交叉能力	模型的训练开销达到了O(n2)的量级，训练开销较大
GBDT+LR	利用GBDT进行“自动化”的特征组合，将原始特征向量转换成离散型特征向量，并输入逻辑回归模型，进行最终的CTR预估	特征工程模型化，使模型具备了更高阶特征组合的能力	无法进行完全的并行训练，模型更新所需的训练时长较长
LS-PLM	首先对样本进行“分片”，在每个“分片”内部构建逻辑回归模型，将每个样本的各个“分片”概率与逻辑回归的得分进行加权平均，得到最终的预估值	模型结构类似三层神经网络，具备了较强的表达能力	模型结构相比深度学习模型仍比较简单，有进一步提高的空间

2006年，矩阵分解的技术成功应用在推荐系统领域，其隐向量的思想与深度学习中Embedding技术的思路一脉相承；2010年，FM被提出，特征交叉的概念被引入推荐模型，其核心思想——特征交叉的思路也将在深度学习模型中被发扬光大；2012年，LS-PLM在阿里巴巴大规模应用，其结构已经非常接近三层神经网络；2014年，Facebook用GBDT自动化处理特征，揭开了特征工程模型化的篇章。

另外，Alex Krizhevsky站在Geoffrey Hinton、Yann LeCun、Yoshua Bengio等大师的肩膀上，于2012年提出了引爆整个深度学习浪潮的AlexNet，将深度学习的大幕正式拉开，其应用快速地从图像扩展到语音，再到自然语言处理领域，推荐系统领域也必然紧随其后，投入深度学习的大潮之中。

从2016年开始，随着FNN、Wide&Deep、Deep Crossing等一大批优秀的推荐模型架构的提出，深度学习模型逐渐席卷推荐和广告领域，成为新一代推荐模型当之无愧的主流。

深度学习在推荐系统中的应用

随着微软的Deep Crossing，谷歌的Wide&Deep，以及FNN、PNN等一大批优秀的深度学习推荐模型在2016年被提出，推荐系统和计算广告领域全面进入深度学习时代。深度学习时代主要在以下两方面取得重大进展：

①深度学习模型的表达能力更强，能够挖掘出更多数据中潜藏的模式

②深度学习的模型结构非常灵活，能够根据业务场景和数据特点，灵活调整模型结构，使模型与应用场景完美契合

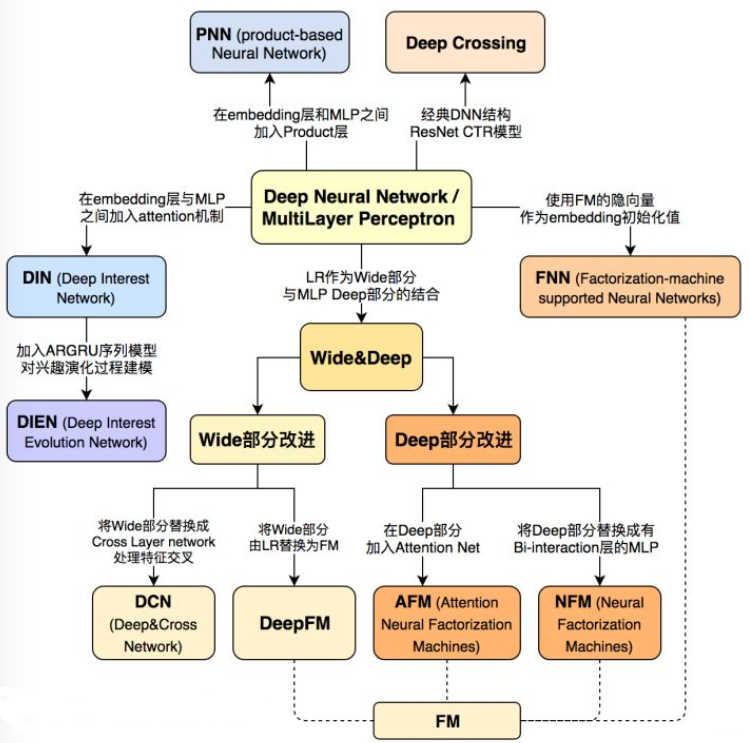
沿着特征工程自动化的思路，深度学习模型从PNN一路走来，经过了Wide&Deep、Deep&Cross、FNN、DeepFM、NFM等模型，进行了大量的、基于不同特征互操作思路的尝试。但特征工程的思路走到这里已经穷尽了可能的尝试，模型进一步提升的空间很小，这也是这类模型的局限性所在。从这之后，越来越多的深度学习推荐模型开始探索更多”结构“上的尝试，诸如注意力机制、序列模型、强化学习等在其他领域大放异彩的模型结构也逐渐进入推荐系统领域，并且在推荐模型的效果提升上成果显著。

一.AutoRec——单隐层神经网络推荐模型

AutoRec在2015年由澳大利亚国立大学提出。它将自编码器（AutoEncoder）的思想和协同过滤结合，提出了一种单隐层神经网络推荐模型。

自编码器的原理类似于协同过滤中的共现矩阵，主成分分析等，相当于在重建函数$h(r； \theta)$中存储了所有数据向量的“精华”。

如上图，AutoRec是一个非常标准的三层神经网络，紫色单隐层的数量k远小于输入/输出评分向量的维度m，所以可以达到“泛化”的效果。

重建函数的具体形式：

$h(r; \theta) = f(W \cdot g(Vr+\mu) + b)$

其中，$f(\cdot)$，$g(\cdot)$分别为输出层神经元和隐层神经元的激活函数。

为防止重构函数的过拟合，在加入L2正则化项后，AutoRec目标函数的具体形式：

$\underset {\theta}{min} \sum^m_{j=1}||r^{(i)}-h(r^{(i)} ; \theta)||^2_O + \cfrac{\lambda}{2} \cdot(||W||^2_F+||V||^2_F)$

由于AutoRec是一个非常标准的三层神经网络，模型的训练利用梯度反向传播即可完成。

AutoRec与协同过滤一样，有基于Item的I-AutoRec（Item based AutoRec），当输入物品$i$的评分向量$r^{(i)}$时，模型的输出向量$h(r^{(i)}; \theta)$就是所有用户对$i$的评分预测。通过遍历，就可以得到一个用户$u$对所有物品的评分预测，进而根据评分预测排序得到推荐列表。U-AutoRec（User based AutoRec）相比I-AutoRec的优势在于仅需输入一次目标用户的用户向量，就可以重建用户对所有物品的评分向量，劣势是用户向量的稀疏性可能会影响模型效果。

总体来说，AutoRec使用一个单隐层的AutoEncoder泛化用户或物品评分，有泛化和表达能力但是并不足。在模型结构上，AutoRec模型和后来的词向量模型(Word2vec)完全一致，但优化目标和训练方法有所不同。

二.Deep Crossing——经典的深度学习框架

Deep Crossing由微软在2016年提出，应用在搜索引擎Bing的搜索广告推荐场景。广告点击率则作为Deep Crossing模型的优化目标，即CTR模型。

Deep Crossing模型特征可以分为三类：一类是可以被处理成one-hot或multi-hot的类别型特征，一类是数值型特征，一类是需要进一步处理的特征，包括广告计划（campaign）、曝光样例（impression）、点击样例（click）等。

为了完成端到端的训练，Deep Crossing解决了以下三个问题：

①稀疏特征稠密化——Embedding层以经典的全连接层（Fully Connected Layer）结构为主，另有衍生出的Word2vec、Graph Embedding等。一般来说，Embedding向量的维度应远小于原始的稀疏特征向量，大多几十到上百维。数值型特征不需要Embedding，直接进入Stacking层。

②自动交叉组合——Multiple Residual Units，相比标准的以感知机为基本单元的神经网络，Deep Crossing采用了多层残差网络（Multi-Layer Residual Network）作为MLP的具体实现。

③输出层达成CTR预测的目标——Scoring层采用sigmoid（图像分类等多分类问题多采用softmax）

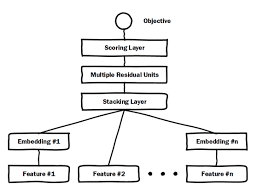
Stacking层比较简单，是把不同的Embedding特征和数值型特征拼接在一起，形成新的包含全部特征的特征向量，该层通常也成为连接层（concatenate）。

残差神经网络

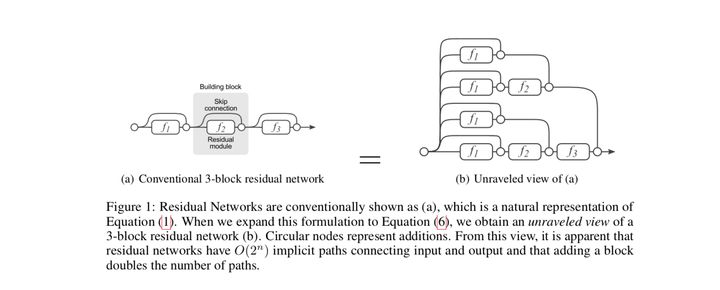
最著名的残差网络是在ImageNet大赛中由微软研究员何凯明提出的152层残差网络。推荐模型中的应用也是残差网络首次在图像识别领域之外的成功推广。残差神经网络就是由残差单元（Residual Unit）组成的神经网络，

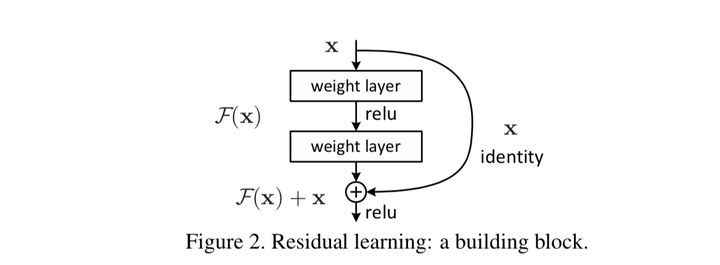
上面的残差单元与传统感知机的区别主要有两个不同：

①输入经过两层以ReLU为激活函数的全连接层后，生成输出向量。

②输入可以通过一个短路（shortcut）通路直接与输出向量进行元素加（element-wise plus）操作，生成最终的输出向量。

此时，残差单元中的两层ReLU网络其实拟合的是输出和输入之间的残差（$x^o-x^i$），这就是残差神经网络名称的由来。

残差神经网络的诞生主要为了解决两个问题：

①神经网络加深后，容易产生过拟合。残差网络中，由于有输入向量短路的存在，很多时候可以越过两层ReLU网络，减少过拟合的发生。

②残差单元使用ReLU激活函数取代sigmoid，越靠近0梯度越大。并且输入向量短路相当于直接把梯度毫无变化地传递到下一层，这也使残差网络收敛速度更快。

三.NeuralCF——CF与深度学习的结合

Embedding层的主要作用是将稀疏向量转换成稠密向量，那么矩阵分解层的用户隐向量和物品隐向量完全可以看作一种Embedding方法。而用户隐向量和物品隐向量的内积操作则可以看作Scoring层。在实际使用矩阵分解来训练和评估模型的过程中，往往会发现模型容易处于欠拟合状态。究其原因是因为矩阵分解的模型结构相对比较简单，特别是Scoring层，无法对优化目标进行有效的拟合。这就要求模型有更强的表达能力，在此动机的启发下，新加坡国立大学的研究人员提出了NeuralCF模型。

NeuralCF用“多层神经网络+输出层”的结构替代了矩阵分解中简单的内积操作。这样做的收益是直观的，一是让用户向量和物品向量做更充分的交叉，得到更多有价值的特征组合信息；二是引入更多的非线性特征，让模型的表达能力更强。

以此类推，事实上，用户和物品向量的互操作层可以被任意的互操作形式所代替，这就是所谓的“广义矩阵分解”模型（Generalized Matrix Factorization）。例如，Scoring元素积+输出层逻辑回归。再进一步，可以把不同互操作网络得到的特征向量拼接起来，交由输出层进行拟合。NeuralCF的论文中给出了整合两个网络的例子：

NeuralCF模型实际上提出了一个模型框架，它基于 用户向量和物品向量这两个Embedding层，利用不同的互操作层进行特征的交叉组合，并且可以灵活地进行不同互操作层的拼接。从这里可以看出深度学习构建推荐模型的优势——利用神经网络理论上能够拟合任意函数的能力，灵活地组合不同的特征，按需增加或减少模型的复杂度。

在实践中要注意：并不是模型越复杂、特征越多越好。一是要防止过拟合的风险，而是往往需要更多数据和更长的训练时间才能使复杂的模型收敛，这需要算法工程师在模型的实用性、实时性和效果之间进行权衡。

NeuralCF模型也存在局限性。由于是基于协同过滤的思想进行构造的，所以NeuralCF模型并没有引入更多其他类型的特征，这在实际应用中无疑浪费了其他有价值的信息。此外，对于模型中互操作的种类并没有做进一步的探究和说明。这就需要后来者进行更深入的探索。

四.PNN——加强特征交叉能力

NeuralCF只提到了用户向量和物品向量两组特征向量，如果加入多组特征向量又该如何设计特征交互的方法呢？2016年，上海交通大学提出的PNN模型，给出了特征交互方式的几种设计思路。

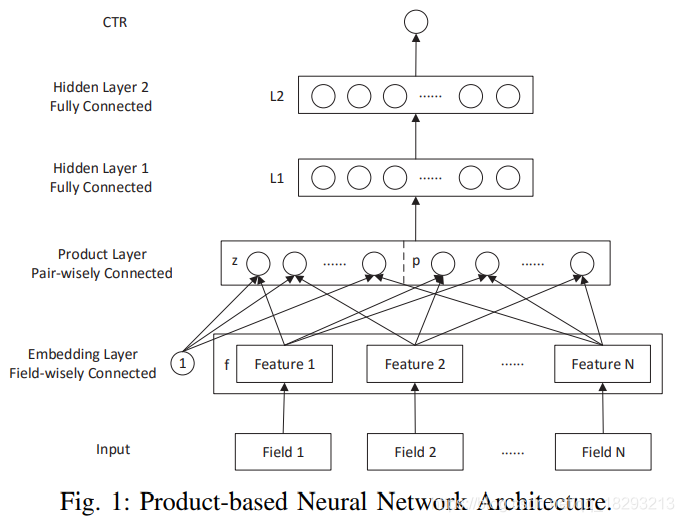
相比Deep Crossing，PNN模型在输入、Embedding层、多层神经网络，以及最终的输出层部分并没有结构上的不同，唯一的区别在于PNN模型用乘积层（Product Layer）代替了Deep Crossing模型中的Stacking层。也就是说，不同特征的Embedding向量不再是简单的拼接，而是用Product操作进行两两相交，更有针对性地获取特征之间的交叉信息。

PNN的Product层的多种特征交叉方式

PNN模型对于深度学习的创新主要在于乘积层的引入。具体地说，PNN模型的乘积层由线性操作部分（上图z部分，对各特征向量进行线性拼接）和乘积操作部分（上图p部分）。其中，乘积特征交叉部分又分为内积操作和外积操作，其中内积操作的PNN模型被称为IPNN（Inner Product-based Neural Network），使用外积操作的PNN模型被称为OPNN（Outer Product-based Neural Network）。

其中外积操作，$g_{outer}(f_i,f_j) = f_if_j^T$，外积互操作生成的是特征向量$f_i,f_j$各维度两两交叉而成的一个$M \times M$的方形矩阵（其中$M$是输入向量的维度）。这样的外积操作无疑会将问题的复杂度从$M$提升到$M^2$，为了一定程度上减少训练负担，PNN模型的论文中介绍了一种降维的方法，就是把所有两两特征Embedding向量外积互操作结果叠加（Superposition），形成一个叠加外积操作矩阵$p$：

$p=\sum^N_{i=1} \sum^N_{j=1}g_{outer}(f_i,f_j) = \sum^N_{i=1} \sum^N_{j=1} f_if_j^T=f_ \sum f_\sum^T,f_\sum=\sum^N_{i=1}f_i$

从公式看，叠加矩阵$p$的最终形式类似于让所有特征Embedding向量通过一个平均池化层（Average Pooling）后，再进行外积互操作。在实际应用中，还应对平均池化操作谨慎对待。因为把不同特征对应维度进行平均，实际上是假设不同特征的对应维度有类似含义。但显然，年龄和地域两个特征在经过各自的Embedding后，两者的Embedding向量不在一个向量空间中，显然不具备任何可比性。这是做平均池化，会模糊很多有价值的信息。平均池化的操作经常发生在同类Embedding上，例如，将用户浏览过的多个物品的Embedding进行平均。因此，PNN模型的外积池化操作也需要谨慎，在训练效率和模型效果上进行权衡。

事实上，PNN模型在对特征的线性和乘积操作后，并没有把结果直接送入上层的$L_1$全连接层，而是在乘积层内部又进行了局部全连接的转换，分别将线性部分$z$，乘积部分$p$映射成了$D_1$维的输入向量$l_z$和$l_p$（$D_1$为$L_1$隐层的神经元数量），再将$l_z$和$l_p$叠加，输入$L_2$隐层。这部分操作不具备创新性，并且可以被其他转换操作完全替代，因此不再详细介绍。

PNN的结构特点在于强调了特征Embedding向量之间的交叉方式是多样化的，相比于简单的交由全连接层进行无差别化的处理，PNN模型定义的内积和外积操作显然更有针对性地强调了不同特征之间的交互，从而让模型更容易捕获特征交叉信息。

但PNN模型同样存在局限性，例如在外积操作时，为了优化$M \times M$的训练效率，对所有特征进行无差别交叉（平均池化），这一定程度上忽略了原始特征向量中包含的有价值信息。如何综合原始特征及交叉特征，让特征交叉的方式更加高效，后续的Wide&Deep模型和基于FM的各类深度学习模型将给出他们的解决方案。

五.Wide&Deep——记忆能力和泛化能力的综合

谷歌于2016年提出Wide&Deep模型，由单层的Wide部分和多层的Deep部分组成的混合模型。其中，Wide部分的作用是让模型具有较强的“记忆能力”（memorization）；Deep部分的主要作用是让模型具有“泛化能力”（generalization），使模型兼具了逻辑回归（简单模型的记忆能力强）和深度神经网络（深度学习网络不断进行的交叉处理，会减弱记忆能力，但会拥有泛化能力）的优点——能够快速处理并记忆大量历史特征，并且具有强大的表达能力，不仅在当时迅速成为业界争相应用的主流模型，而且衍生出了大量以Wide&Deep模型为基础结构的混合模型，影响力一直延续至今。

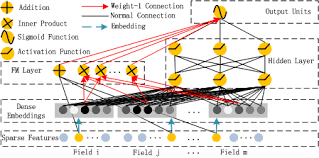
Wide&Deep模型把单输入层的Wide部分与由Embedding层和多隐层组成的Deep部分连接起来，一起输入最终的输出层（逻辑回归）。其中Wide部分善于处理大量稀疏特征，而Deep部分善于挖掘特征背后的数据模式。这种把不同特征使用不同处理方法的组合模型，就需要对业务场景的深刻理解。从下图可以详细地了解到Google Play的推荐团队到底将哪些特征作为Deep输入，哪些作为Wide部分输入。

Deep部分输入全量的特征向量，拼接成1200维的Embedding向量，再经过3层ReLU全连接层，最终输入LogLoss输出层。

Wide部分输入仅仅是已安装应用和曝光应用两类特征，其中已安装应用代表用户的历史行为，而曝光应用代表当前的待推荐应用。选择这两类特征的原因是充分发挥Wide部分的记忆能力，使用简单模型善于记忆用户行为特征中的信息，并根据此类信息直接影响推荐结果。

Wide部分组合“已安装应用”和”曝光应用“两个特征的函数被称为交叉积变换（Cross Product Transformation）函数，其形式化定义如：

$\phi_k(X)= \prod_{i=1}^{d}x_i^{c_ki}$ $c_{ki} \in {0,1}$

$c_{ki}$是一个布尔变量，当第$i$个特征属于第$k$个组合特征时，$c_{ki}$的值为1，否则为0；$x_i$是第$i$​个特征的值。例如，对于”AND(user_installed_app=netflix, impression_app=pandora)“这个组合特征来说，只有当"user_installed_app=netflix"和”impression_app=pandora“这两个特征同时为1时，其对应的交叉积变换层的结果才为1，否则为0。

在通过交叉积变换层操作完成特征组合之后，Wide部分将组合特征输入最终的LogLoss输出层，与Deep部分的输出一同参与最后的目标拟合，完成Wide与Deep的融合部分。

Wide&Deep开启了不同网络融合的新思路，日后有比较经典的2017年由斯坦福大学和谷歌的研究人员提出的Deep&Crossing模型。其主要思路是使用Cross网络替代原来的Wide部分。

使用Cross网络的目的是增加特征之间的交互力度，使用多交叉层（Cross layer）对输入向量进行特征交叉。假设第$l$层交叉层的输出向量为$x_l$，那么第$l+1$层的输出向量：

$x_{l+1}=x_0x_l^TW_l + b_l + x_l$

可以看到，交叉层操作的二阶部分类似于PNN模型中的外积操作，在此基础上增加了外积操作的权重向量$w_l$，以及原输入向量$x_l$和偏置向量$b_l$。

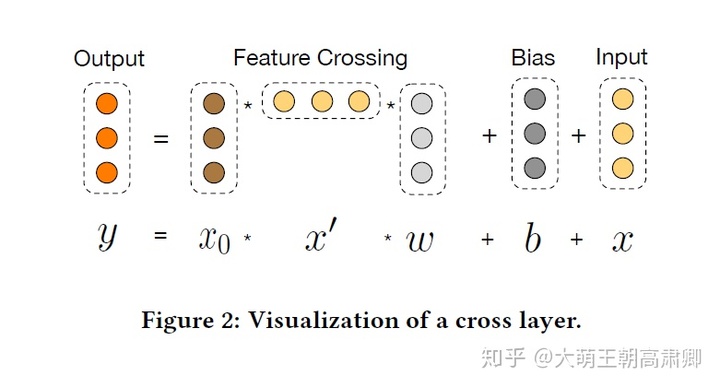
可以看出，Cross层在参数方面是比较”克制“的，每一层仅增加了一个$n$维的权重向量$w_l$（n维输入向量维度），并且在每一层均保留了输入向量，因此输入与输出之间变化不会非常明显。由多层交叉层组成的Cross网络在Wide&Deep模型中的Wide部分的基础上进行特征的自动化交叉，避免了很多基于业务理解的人工特征组合。同Wide&Deep模型一样，Deep&Cross模型的Deep部分相比Cross部分表达能力更强，使模型具备更强的非线性学习能力。

Wide&Deep模型的影响力无疑是巨大的，不仅是其本身成功应用于多家一线互联网公司，而且其后续的改进创新工作也延续至今。事实上，DeepFM、NFM等模型都可以看成Wide&Deep模型的延伸：

Wide&Deep模型能够取得成功的关键在于：

①抓住了业务问题的本质特点，能够融合传统模型记忆能力和深度学习模型泛化能力的优势

②模型的结构并不复杂，易于工程实现、训练和上线，这加速了业界推广

也正是从Wide&Deep模型之后，越来越多的模型结构被加入推荐模型中，深度学习模型的结构开始朝着多样化、复杂化的方向发展。

六.FM与深度学习的结合

FNN——用FM的隐向量完成Embedding层初始化

FNN由伦敦大学学院的研究人员于2016年提出，以FM改进Embedding层的Deep crossing模型，用FM模型训练好的各特征向量初始化Embedding层的参数代替随机初始化，相当于在初始化神经网络参数时，已经引入了有价值的先验信息。也就是说，神经网络训练的起点更接近目标最优点，自然加速了整个神经网络的收敛过程。

一般情况下，模型的收敛速度往往受限于Embedding层。主要有两个原因：①Embedding层的参数量巨大。假设输入层维度维100,000，Embedding层输出维度为32，上层再加5层32维的全连接层，最后输出层维度为10，那么输入层到Embedding层的参数数量是$32 \times100,000=3,200,000$，其余所有层的参数总数是$(32 \times 32) \times4+32\times 10 = 4416$​。此时Embedding层参数占比99.86%。这就导致大部分的训练时间和计算开销都被Embedding层占据。②由于输入向量过于稀疏，在随机梯度下降时，只有与非零特征相连的Embedding层权重会被更新，这进一步降低了Embedding层的收敛速度。

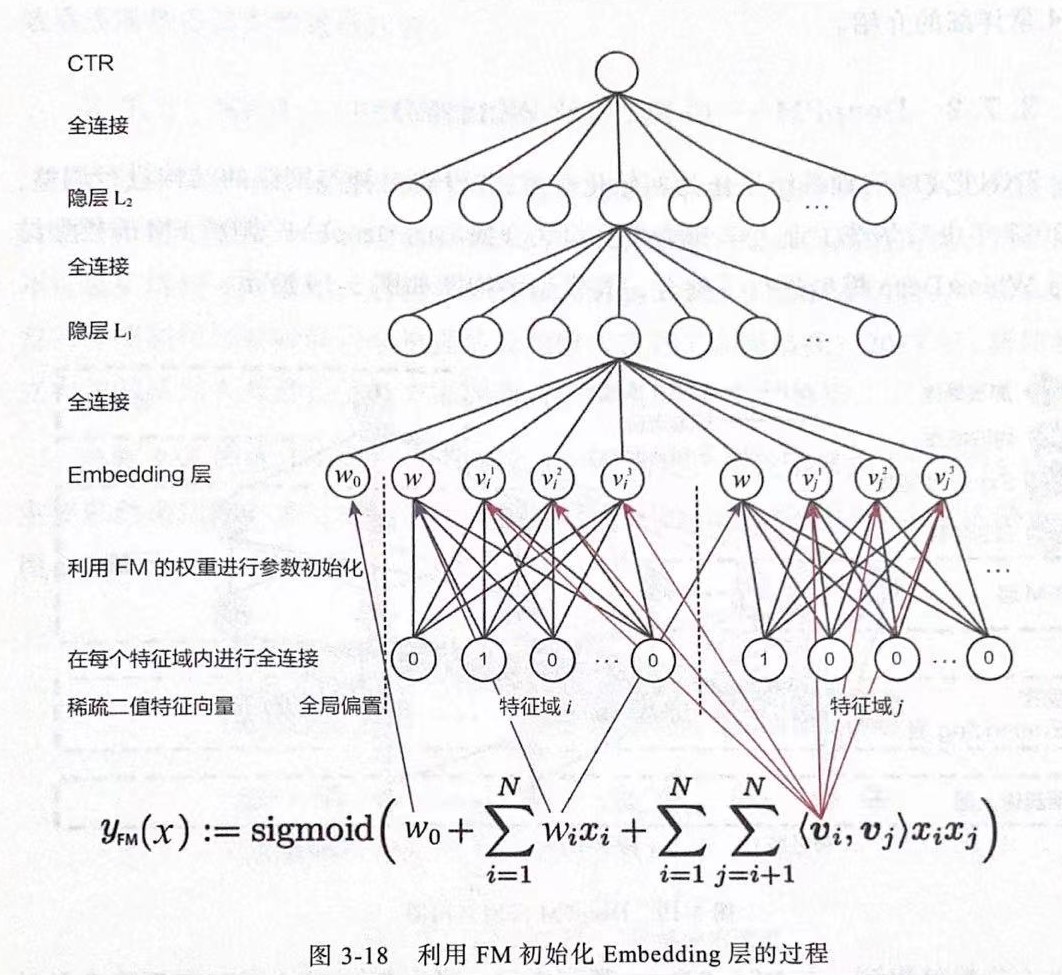
需要说明的是，在训练FM的过程中，并没有对特征域进行区分，但在FNN模型中，特征被分成了不同特征域，因此每个特征域具有对应的Embedding层，并且每个特征域Embedding的维度都应与FM隐向量维度保持一致。

DeepFM——用FM代替Wide部分

FNN把FM的结果作为初始化权重，并没有调整模型结构。而2017年由哈尔滨工业大学和华为公司联合提出的DeepFM则将FM模型与Wide&Deep模型整合：

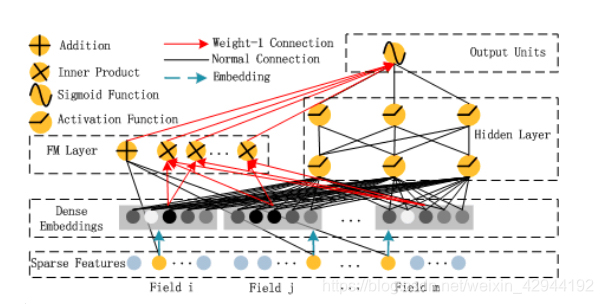
FM部分与深度神经网络部分共享相同的Embedding层。左侧FM部分对不同的特征域的Embedding进行两两交叉，也就是将Embedding向量当作原FM中的特征隐向量。最后将FM的输出与Deep部分的输出一同输入最后的输出层，参与最后的目标拟合。

DeepFM与Deep&Cross模型完全一致，唯一的不同在于Deep&Cross利用多层Cross网络进行特征组合，而DeepFM模型利用FM进行特征组合。当然，具体的应用效果还需要通过实验进行比较。

NFM——FM的神经网络化尝试

无论是FM还是FFM，归根结底是一个二阶特征交叉的模型，受组合爆炸问题的困扰，FM几乎不可能扩展到三阶以上，这就不可避免地限制了FM模型的表达能力。2017年，新加坡国立大学的研究人员进行了这方面的尝试，提出了NFM模型。

NFM模型的主要思路是用一个表达能力更强的函数替代原FM中二阶隐向量内积的部分：

$\hat{y}{NFM}(x)=w_0 + \sum^N{i=1}w_ix_i+f(x)$

传统机器学习可以用来拟合$f(x)$一个表达能力更强的函数，但是进入深度学习时代后，由于深度学习网络理论上有拟合任何复杂函数的能力，$f(x)$的构造工作可以交由某个深度学习网络来完成，并通过梯度反向传播来学习。

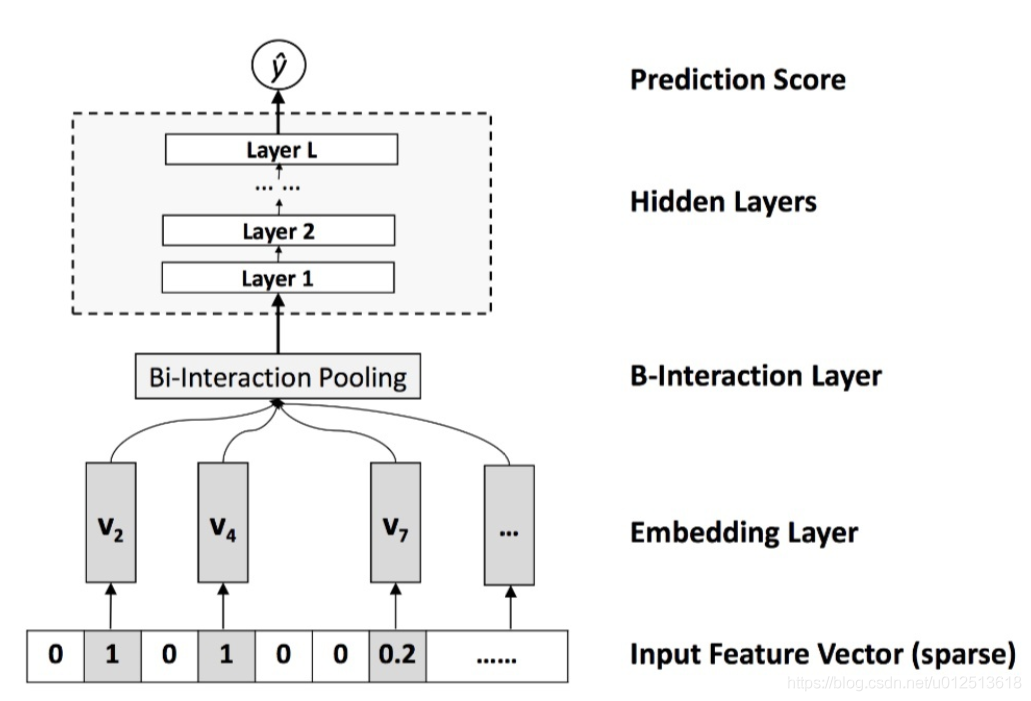
NFM网络架构的特征非常明显，就是在Embedding和神经网络之间加入特征交叉池化层（Bi-Interaction Pooling Layer）：

$f_{BI}(V_x)=\sum^n_{i=1} \sum^n_{j=i+1}(x_iv_i)\bigodot(x_jv_j)$

其中，$\bigodot$代表元素积操作，其中第k维的操作：

$(v_i\bigodot v_j)k=v{ik}v_{jk}$

在进行两两元素积操作后，对交叉特征向量取和，得到池化层的输出向量。再把该向量输入上层的多层全连接神经网络，进行进一步的交叉。

上图的NFM省略了一阶部分，如果把一阶部分视为一个线性模型，那么NFM的架构也可以视为Wide&Deep模型的进化。相比原始的Wide&Deep模型，NFM模型对其Deep部分加入了特征交叉池化层，加强了特征交叉。这是理解NFM模型的另一个角度。

七.注意力机制在推荐模型中的应用

“注意力机制”来源于人类最自然的选择性注意的习惯，从2017年开始，推荐领域也开始尝试将注意力机制引入模型之中，这其中影响力较大的工作是由浙江大学提出的AFM和由阿里巴巴提出的DIN。这一机制堆深度学习推荐系统的启发是重大的，使得其更接近用户真实的思考过程。

AFM——引入注意力机制的NFM

在NFM模型中，不同域的特征Embedding向量经过特征交叉池化层的交叉，将各交叉特征向量进行“加和”，输入最后由多层神经网络组成的输出层。AFM模型引入注意力机制是通过在特征交叉层和最终的输出层之间加入注意力网络（Attention Net）实现的。AFM的模型结构图：

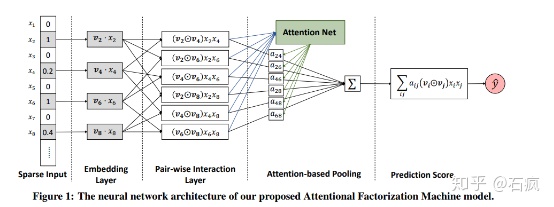
注意力网络的作用是为每一个交叉特征提供权重，也就是注意力得分。

同NFM一样，AFM的特征交叉过程同样采用了元素积操作：

$f_{PI}(\varepsilon){(v_i\bigodot v_j)x_ix_j}_{(i,j)\in R_x}$

引入注意力得分后的池化过程：

$f_{Att}(f_{PI}(\varepsilon)) = \sum_{(i,j) \in R_x} a_{ij}(v_i\bigodot v_j)x_ix_j$​

对注意力的分$a_{ij}$来说，最简单的方法就是用一个权重参数来表示，但为了防止交叉特征数据稀疏问题带来的权重参数难以收敛，AFM模型使用了一个在两两特征交叉层（Pair-wise Interaction Layer）和池化层之间的注意力网络来生成注意力得分。 该注意力网络的结构是一个简单的单全连接层加softmax输出层的结构：

$a^`_{ij}=h^TReLU(W(v_i\bigodot v_j)x_ix_j+b)$

$a_{ij}=\cfrac{exp(a^_{ij})}{\sum_{(i,j)\in R_x} exp(a^_{ij})}$

其中需要学习的参数是特征交叉层到注意力网络全连接层的权重矩阵$W$，偏置向量$b$，以及全连接层到softmax输出层的权重向量$h$。注意力网络将与整个模型一起参与梯度反向传播的学习过程，得到最终的权重参数。

AFM是研究人员从改进模型角度进行的一次尝试。而阿里巴巴引入注意力机制是基于其对业务观察的一次模型改进，下面介绍阿里巴巴在业界非常知名的推荐模型DIN。

DIN——引入注意力机制的神经学习网络

它的应用场景是阿里巴巴的电商广告推荐，在计算一个用户$u$是否点击一个广告$a$时，模型的输入特征自然分为两大部分：一部分是用户$u$的特征组，另一部分是候选广告$a$的特征组。无论是用户还是广告，都含有两个非常重要的特征——商品id(good_id)和商铺id(shop_id)。用户特征里的商品特征是一个序列，代表用户曾点击过的商品合集，商铺id同理；而广告特征里的商品id和商铺id就是广告对应的商品id和商铺id（阿里巴巴平台上的广告大部分是参与推广计划的商品）。

在原来的基础模型中，这些特征进行简单的平均池化操作就后就进入上层神经网络进行下一步训练，序列中的商品既没有区分重要程度，也和广告特征中的商品id没有关系。

然而事实上，广告特征和用户特征的关联程度是非常强的，假设广告中的商品是键盘，那么用户点击商品序列中的不同商品id：鼠标、T恤和洗面奶。从常识出发，鼠标这个历史商品对预测键盘广告的点击率的重要程度远大于后两者。从模型角度，基于不同特征的注意力理应不同，而且“注意力得分”的计算理应与广告特征有相关性。

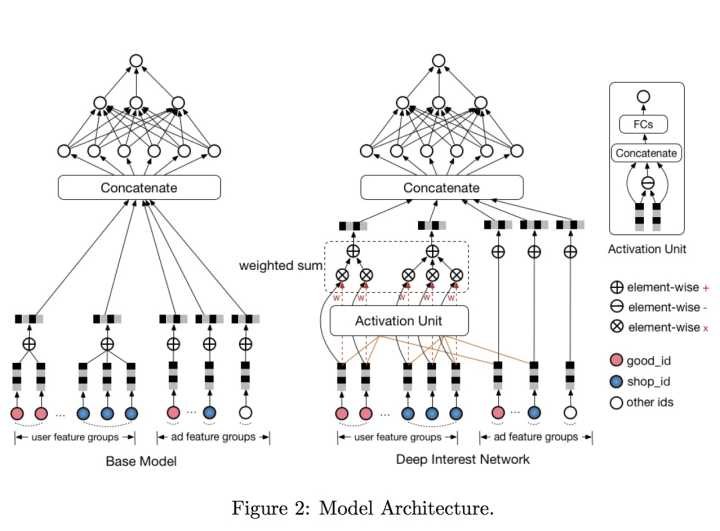
模型中的注意力的强弱，利用候选商品和历史行为商品之间的相关性计算出一个权重，这个权重就代表了“注意力”强弱：

$V_u=f(V_a)=\sum ^N_{i=1}w_i \cdot V_i=\sum ^N_{i=1}g(V_i,V_a) \cdot V_i$

其中$V_u$是用户的Embedding向量，$V_a$是候选广告商品的Embedding向量，$V_i$是用户$u$的第$i$次行为的Embedding向量。这里用户的行为就是浏览商店或店铺，因此行为的Embedding向量就是那次浏览的商品或店铺的Embedding向量。$g(V_i,V_a)$即注意力得分函数采用一个注意力激活单元（activation unit）。其本质上也是一个小的神经网络，其具体结构如上图右上角。可以看出，激活单元的输入层是两个Embedding向量，经过元素减（element-wise minus）操作后，与原Embedding向量一同连接后形成全连接层的输入，最后通过单神经元输出层生成注意力得分。

DIEN——序列模型与推荐系统的结合

从“注意力机制”开始，越来越多对深度学习模型结构的改进是基于对用户行为的深刻观察而得出。DIEN基于DIN，创新在于用序列模型模拟了用户兴趣的进化过程。序列信息的重要性在于：①加强了最近行为对下次行为预测的影响。②能够学习到购买趋势的信息，如果某个转移概率在全局统计意义上足够高——购买过篮球鞋后购买机械键盘的概率，那么在用户购买篮球鞋时，推荐机械键盘也会成为一个不错的选择。直观上，两者的用户群体很有可能是一致的。

如果失去序列信息，推荐模型则是基于用户购买历史的综合推荐，而不是针对“下一次购买”的推荐，显然，从业务角度看，后者才是推荐系统正确的推荐目标。

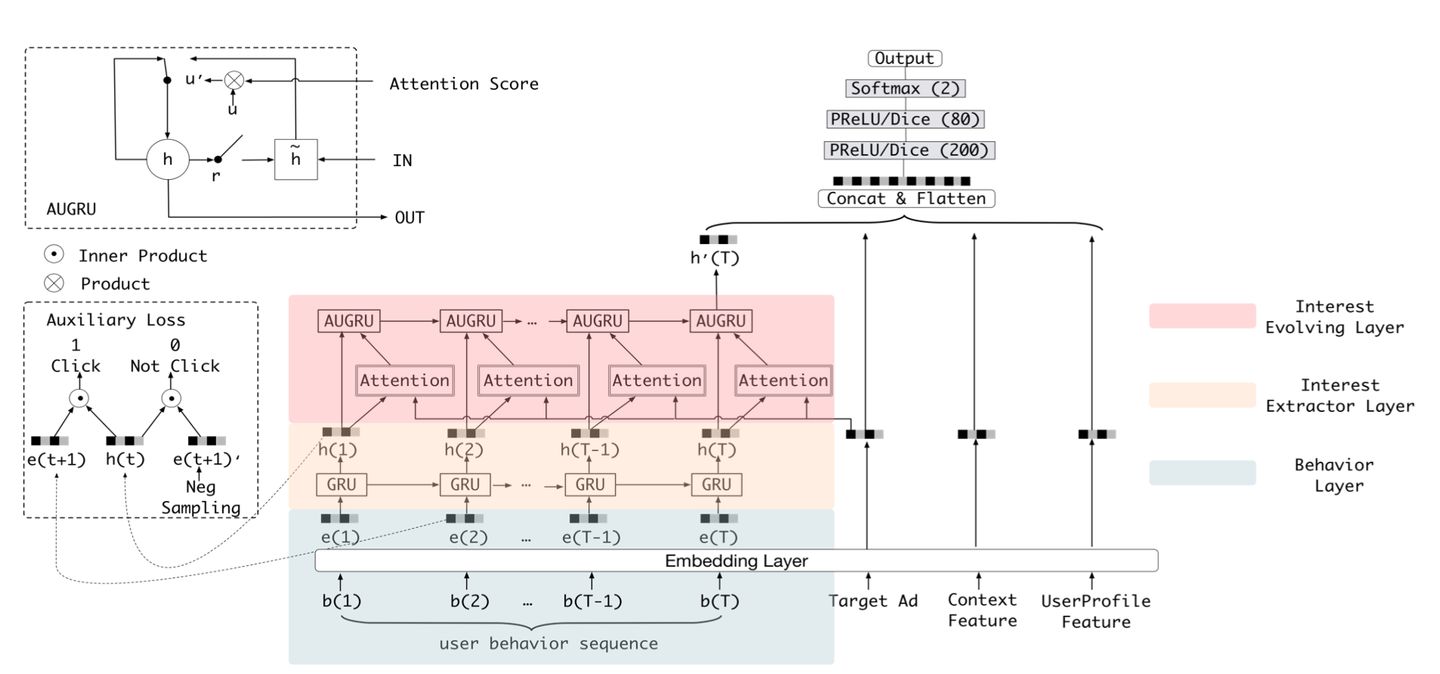
其中兴趣进化网络分为三层，从下至上依次是：

①行为序列层（Behavior Layer，浅绿色部分）：其主要作用是把原始的id类行为序列转换成Embedding行为序列。

②兴趣抽取层（Interest Extractor Layer，米黄色部分）：其主要作用是通过模拟用户兴趣迁移过程，抽取用户兴趣。

③兴趣进化层（Interest Evolving Layer，浅红色部分）：其主要作用是通过在兴趣抽取层基础上加入注意力机制，模拟与当前目标广告相关的兴趣进化过程。

在兴趣进化网络中，行为序列层的结构与普通的Embedding层是一致的，模拟用户兴趣进化的关键在于“兴趣抽取层”和“兴趣进化层”。

兴趣抽取层的基本结构是GRU（Gated Recurrent Unit）

本章介绍了以下模型，但深度学习推荐模型从没停下他前进的脚步。从阿里巴巴的多模态、多目标的深度学习模型，到Youtube基于session的推荐系统，再到Airbnb使用Embedding技术构建的搜索推荐模型，深度学习推荐模型不仅进化速度越来越快，而且应用场景也越来越广。在之后的章节中，笔者会从不同的角度出发，介绍深度学习模型再推荐系统中的应用，也希望读者可以在本章的知识结构上，跟踪最新的深度学习推荐模型进展。

模型名称	基本原理	特点	局限性
AutoRec	基于自编码器，对用户或者物品进行编码，利用自编码器的泛化能力进行推荐	单隐层神经网络结构简单，可实现快速训练和部署	表达能力较差
Deep Crossing	利用“Embedding层+多隐层+输出层”的经典深度学习框架，预完成特征的自动深度交叉	经典的深度学习推荐模型框架	利用全连接隐层进行特征交叉，针对性不强
NeuralCF	将传统的矩阵分解中用户向量和物品向量的点积操作，换成由神经网络代替的互操作	表达能力加强版的矩阵分解模型	只使用了用户和物品的id特征，没有加入更多其它特征
PNN	针对不同特征域之间的交叉操作，定义“内积”“外积”等多种积操作	在经典深度学习框架上提高特征交叉能力	“外积”操作进行了近似化，一定程度上影响了其表达能力
Wide&Deep	利用Wide部分加强模型的“记忆能力”，利用Deep部分加强模型的“泛化能力”	开创了组合模型的构造方法，对深度学习推荐模型的后续发真产生重大影响	Wide部分需要人工进行特征组合的筛选
Deep&Cross	用Cross网络替代Wide&Deep模型中的Wide部分	解决了Wide&Deep模型人工组合特征的问题	Cross网络的复杂度较高
FNN	利用FM的参数来初始化深度神经网络的Embedding层参数	利用FM初始化参数，加快整个网络的收敛速度	模型的主结构比较简单，没有针对性的特征交叉层
DeepFM	在Wide&Deep模型的基础上，用FM替代原来的线性Wide部分	加强了Wide部分的特征交叉能力	与经典的Wide&Deep模型相比，结构差别不明显
NFM	用神经网络代替FM中二阶隐向量交叉的操作	相比FM,NFM的表达能力和特征交叉能力更强	与PNN模型的结构非常相似
AFM	在FM的基础上，在二阶隐向量交叉的基础上对每个交叉结果加入了注意力得分，并使用注意力网络学习注意力得分	不同交叉特征的重要性不同	注意力网络的训练过程比较复杂
DIN	在传统深度学习推荐模型的基础上引入注意力机制，并利用用户行为历史物品和目标广告物品的相关性计算注意力得分	根据广告物品的不同，进行更有针对性的推荐	并没有充分利用除“历史行为”以外的其他特征
DIEN	将序列模型与深度学习推荐模型结合，使用序列模型模拟用户的兴趣进化过程	序列模型增强了系统对用户兴趣变迁的表达能力，使推荐系统开始考虑时间相关的行为序列中包含的有价值信息	序列模型的训练复杂，线上服务的延迟较长，需要进行工程上的优化
DRN	将强化学习的思路应用于推荐系统，进行推荐模型的线上实时学习和更新	模型对数据实时性的利用能力大大加强	线上部分较复杂，工程实现难度较大

\未完待续。。。:)

异常值指通常明显地不同于数据集中其他数据。有些异常值由于自然本身存在特殊情况，一些异常值由于统计失误，无论如何异常点的存在都会扭曲数据集的数据分布，提高数据的不连贯性或使观测产生错误。 为了使训练模型在进行测试时有更好的泛用性，识别并处理异常点非常重要，识别异常值的方法有简单统计分析、3δ原则、z-score及箱型图等。 识别后处理这些异常值的理想方法就是找出引起这些异常值的原因。 处理它们的方法将取决于它们发生的原因，异常值的原因可以分为两大类：人为错误和自然错误。 根据不同原因： 1.删除含有异常值的记录 2.将异常值视为缺失值，交给缺失值处理方法来处理 3.用平均值来修正 4.对于自然异常值且判断可以为模型提供正向训练信息的异常值可以不处理