本书基本上算是我自然语言处理方向的启蒙读物,虽然之后研究生读了机器学习,没有选择自然语言处理,但是无论是在学习中还是工作中,都还是会接触一些相关应用。当然,这本书是一本科普读物,至少在仅有的我熟悉的几章中,书中的介绍还是比较基础的模型(当然这正是现在复杂模型的数学基础)。另外,这是一本让你构建宏观体系的书,它介绍了人工智能运用在工业界的方方面面,让人们对这些问题的解决有一个“道”的思想理解,有趣的是,因为这种宏观的描绘,在读书中会有很多背后蕴藏的深刻理论会吸引你停下读书的脚步,对其进行更深的探索,这正是本书的乐趣所在。
在此记录读书中的收获和积累,也希望给无暇读书的同行一个十分钟读完本书的可能。
①统计语言模型
当前词的概率只取决于前面N-1个词,这种假设被称为N-1阶马尔可夫假设,对应的语言模型称为N元模型(N-Gram Model)。N = 2的二元模型就只取决于前一个词,而N = 1的一元模型实际上是一个上下文无关的模型,也就是假定当前词出现的概率与前面的词无关。而在实际中,应用最多的是N=3的三元模型,更高阶的模型就很少使用。
为什么N取值一般都这么小呢?这里主要有两个原因。首先,N元模型的大小(或者说空间复杂度)几乎是N的指数函数,即O(|V|^N ),这里|V|是一种语言词典的词汇量,一般在几万到几十万个。而使用N元模型的速度(或者说时间复杂度)也几乎是一个指数函数,即O(|V|^(N−1) )。因此,N不能很大。而且当模型从3到4时,效果的提升就不是很显著了,但资源的耗费却增加的非常快,所以,除非是为了做到极致不惜资源,很少有人使用四元以上的模型。Google的罗塞塔翻译系统和语音搜索系统,使用的就是四元模型,该模型存储于500台以上的Google服务器中。
另外,因为上下文之间的相关性可能跨度非常大,甚至可以从一个段落到另一个段落,所以N无论多大都不能覆盖所有的语言现象。这就需要一些长程的依赖性(Long Distance Dependency)来解决问题了。
而重新估算概率的估计使用古德-图灵估计(Good-Turing Estimate),模型的零概率及较小统计值的平滑问题卡茨退避法(Katz Backoff),一般参数T在8-10之间,频数在T以上的词不用进行古德-图灵估计,同时为了保证总概率为1,所有下调频率总和平均分给未出现的词,内伊(Herman Ney)等人对卡茨退避法进行了一次优化,原理大同小异,参考。PS.二元组的相对频率比三元组更接近概率分布,低阶模型比高阶模型零概率问题轻微,因此用低阶语言模型和高阶语言模型进行线性插值来达到平滑目的,这种方法称为删除差值(Deleted Interpolation),此方法比卡茨退避法略差,现在已经很少用了。
需要训练数据和应用数据一致且训练量足够大,所以在语料少的情况下,片面追求高阶的大模型没什么意义。另外,训练语料的噪音高低也会产生影响,因此,一般情况下,对于能找到模式(Pattern)的、量比较大的噪音还是有必要过滤的,比如网页文本中存在的大量制表符。
②谈谈分词
分词问题属于已经解决的问题,在工业界,只要采用基本的统计语言模型,加上一些业界熟知的技巧就能得到很好的分词结果,提高的空间微乎其微(人工分词也有不同的差异)。另外,在手写体识别中,罗马体系的拼音语言也需要分词方法。
梁南元教授提出的“查字典”这种最简单的方法可以解决七八成以上的分词问题,1990年前后,郭进博士用统计语言模型成功解决了分词二义性问题,即各种不同的分词方式中,出现概率最高的分词方法。但是,如果穷举所有可能的分词方法并计算出每种可能性下句子的概率,那么计算量是相当大的。因此,可以把它看成是一个(Dynamic Programming)的问题,并利用维特比(Viterbi)算法快速地找到最佳分词。接下来,孙茂松教授解决了没有字典时的分词问题,吴德凯教授最早将中文分词方法用于英文词组的分割,并且将英文词组和中文词组在机器翻译时对应起来。
词的颗粒度问题,在机器翻译中,颗粒度大效果好,而在搜索中,颗粒度小效果好,因为当用户查询清华时,我们时希望能找到清华大学的。对于上述大小粒度的需求,我们可以构造一个分词器同时支持不同层次的分词—基于基本词表与复合词表,根据基本词表和复合词表分别建立语言模型–L1和L2。这就是分词的层次概念。
分词的不一致性可以分为错误和颗粒度不一致两种,错误又分成两类,一类是越界错误,比如把“北京大学生”分成“北京大学-生”。另一类是覆盖型错误,比如把“贾里克尼”拆成四个字。这些是明显的错误,是改进分词器时要尽可能消除的。接下来是颗粒度的不一致性,人工分词的不一致性大多属于此类。这一类不一致性在衡量分词器的好坏时,可以不作为错误。对于某些应用,需要尽可能地找到各种复合词,而不是将其切分。总之,要继续做数据挖掘,不断完善复合词的词典(它的增长速度较快),这也是近年来中文分词工作的重点。
③信息的度量和作用
变量的不确定性越大,熵也就越大,所需信息量就越大。一本50万字的中文书平均有多少信息量,常用的前10%的汉字占常用文本的95%以上,那么每个汉字的信息熵约8-9bit,如果考虑上下文,每个汉字的信息熵就只有5bit左右。所以一本50万字的中文书,信息量大约是250万比特,采用较好的算法进行压缩,整本书可以存成一个320kb的文件,而如果直接用两字节的国标编码存储这本书,大约需要1MB大小,是压缩文件的3倍,这两个数量的差距,在信息论中被称作“冗余度”(Redundancy),需要指出的是,这里的250万比特是个平均数,同样长度的书,所含的信息量可以差很多。如果一本书重复内容很多,它的信息量就小,冗余度就大。而在不同语言中,汉语是冗余度相对小的。
一个事物的不确定性U,需要引入信息I来消除,而需要引入的信息量取决于这个不确定性的大小,即I>U才行。在某些时候,不引入新的信息,而在已有的信息上玩数字和公式的游戏,本质上和蒙没有区别。
说回自然语言的统计模型,其中一元模型就是通过某个词本身的概率分布来消除不确定性,而二元及更高阶的语言模型则还使用了上下文的信息,这些“相关的”信息可以消除不确定性,就像ID3树模型中使用的节点选择依据–条件熵,也是根据条件熵体现某个特征对目标变量取值的判断是否有消除不确定性的作用。所以说,自然语言处理的大量问题就是寻找相关信息。
还是使用决策树节点选择作为例子,为了度量一个特征(信息)对目标特征(目标信息)的相关性,或者说消除目标信息不确定性的能力,我们使用互信息,而互信息就是目标特征的不确定性(熵)-条件熵(在已知某特征时目标特征的不确定性),当X和Y完全相关时,它的取值时H(X),同时H(X)=H(Y),当两者完全无关时,它的取值是0。
信息论中的另一个重要概念,相对熵,又叫交叉熵,是机器学习分类模型中经常使用的损失函数。相对熵也用来度量相关性,但和变量的互信息不同,它用来衡量两个取值为正数的函数的相似性。交叉熵是不对称的,詹森和向明提出了一种新的相对熵的计算方法,将其左右取平均,在Google的自动问答系统中,我们采用了上面的詹森-香农度量来衡量两个答案的相似性。相对熵还可以用来衡量两个常用词(在语义和语法上)在不同文本中的概率分布,看它们是否同义。另外,利用相对熵,还可以得到信息检索中最重要的一个概念:词频率-逆向文档频率(TF-IDF)。
总的来说,熵、条件熵和相对熵这三个概念与语言模型的关系非常密切。贾里尼克从条件熵和相对熵出发,定义了一个称为语言模型复杂度(Perplexity)的概念来直接衡量语言模型的好坏。复杂度有很清晰的物理含义,它是在给定上下文的条件下,句子中每个位置平均可以选择的单词数量。一个模型的复杂度越小,每个位置的词就越确定,模型越好。
李开复博士介绍他发明的Sphinx语音识别系统的论文里谈到,如果不用任何语言模型(即零元语言模型),(模型的)复杂度为997,也就是说句子中每个位置有997个可能的单词可以填入。如果(二元)语言模型只考虑前后词的搭配,不考虑搭配的概率,复杂度为60。虽然它比不用语言模型好很多,但与考虑搭配概率的二元语言模型相比要差很多,因为后者的复杂度只有20。
④贾里尼克和现代语言处理
20世纪70年代的IBM,在其他科学家把语音识别问题当作人工智能和模式匹配问题时,贾里尼克等人在IBM把它当作通信问题,并用两个隐马尔可夫模型(声学模型和语言模型)把语音识别概括得清清楚楚。
贾里尼克和波尔、库克以及拉维夫的另一大贡献是BCJR算法,这是今天数字通信中应用最广的两个算法之一(另一个是维特比算法)。
⑤简单之美-布尔代数和搜索引擎
Truth is ever to be found in simplicity, and not in the multiplicity and confusion of things.
布尔代数对于数学的意义等同于量子力学对于物理学的意义。他们将我们对世界的认知从连续状态扩展到离散状态。
搜索引擎通过建立索引来在零点零几秒内就找到成千上万甚至上亿的结果。早期的文献检索查询系统,严格要求查询语句复合布尔运算。相比之下,今天的搜索引擎会聪明的自动把用户的查询语句转换成布尔运算的算式,但是基本的原理没有什么不同。
就像我们理解的ES倒排索引进行搜索的原理一样,如果要找到同时包含“原子能”和“应用”的文章,只要将代表是否有这两个字的二进制数组进行布尔运算AND,就可以得到结果。例如“原子能”的布尔数组为10001,表示第一篇和第五篇文章包含原子能关键字。“应用”的布尔数组为01001,那么同时包含“原子能”和“应用”的文章就是00001,即第五篇文章。
对于互联网的搜索引擎来说,每一个网页就是一个文献。这个索引是巨大的,在万亿字节这个量级。早期的搜索引擎(比如AltaVista以前的所有搜索引擎),由于受计算机速度和容量的限制,只能对重要、关键的主题词建立索引,但是这样不常见的词和太常见的虚词就找不到了。现在,为了保证对任何搜索都能提供相关的网页,常见的搜索引擎都会对所有的词进行索引。但是,这在工程上却极具挑战性。
加入互联网上有10^10^个有意义的网页,而词汇表的大小是30万,那么这个索引的大小至少是(10^10^)*30=3000万亿。考虑到大多数词只出现在一部分文本中,压缩为30万亿的量级。为了网页排名方便,索引中还需存有大量附加信息,如这个词出现的位置、次数等。因此,整个索引会通过分布式的方式根据网页的序号将索引分成很多份(Shards),分别存储在不同服务器中。同时,为了提高效率,需要根据网页的重要性、质量和访问的频率建立常用的非常用等不同级别的索引。常用的索引需要访问速度快,附加信息多,更新也要快;而非常用的要求就低多了。但是不论搜索引擎的索引在工程上如何复杂,原理上依然非常简单,即等价于布尔运算。
⑥图论和网络爬虫
上文提到搜索引擎,主要由下载、索引和排序组成,布尔代数支撑了索引的逻辑,那么图论中的遍历算法支撑了搜索引擎的下载。
对于图论相关算法有很多,图的遍历、最短路径、MST、Floyd算法等。而基于图论,还有许多Np-Hard的有趣问题如TSP、VRP问题等。
假定从一家门户网站的首页出发,先下载这个网站,然后通过分析这个网站,可以找到页面里的所有超链接,也就等于知道了这家门户网站首页所直接链接的全部网页。让计算机不停搜索下去,就能下载整个互联网。在网络爬虫中,人们使用Hash Table来记载哪些网站已经被访问过。现在的互联网非常庞大,一个商业的网络爬虫需要有成千上万个服务器,并且通过高速网络连接起来。如何建立起这样复杂的网络结构,如何协调这些服务器的任务,就是网络设计和程序设计的艺术了。
网络爬虫对网页遍历的次序不是简单的BFS或DFS,而是有一个相对复杂的下载优先级排序方法,由调度系统(Scheduler)管理。在调度系统里需要存储那些已经发现但尚未下载的URL,它们一般存在一个优先级队列(Priority Queue),这在工程上与BFS更相似,因此,爬虫中BFS的成分多一些。
对于页面的分析,过去由HTML书写的网站很容易提取,但是现在很多网页是由一些脚本语言(如JavaScript)生成。打开网页的源代码,URL不是直接可见的文本,而是运行这一段脚本才能得到的结果。因此网络爬虫需要模拟运行这一段脚本。另外,有些脚本写的非常不规范,以至于解析起来非常困难(浏览器可以解析),这就需要解析人员具有非常强大的浏览器内核工程能力。因此,如果一些网页明明存在,但搜索引擎没有收录,一个原因可能是网络爬虫中的解析程序没能成功解析网页中不规范的脚本程序,又或者这个网页搞了反爬(就像GitHub.io的博客)。
上面提到过,Hash Table被用来记录哪些网站已经被访问过,Hash Table判断一个网页是否在表中只需要1个复杂度,写入某新网站也只需要Hash运算。但在一个成千上万个服务器的爬虫工程中,存储并实时维护一张哈希表就是一个令人头疼的事了。为了各个服务器不做重复的工作,它们需要在下载前和下载后实时访问哈希表,这就造成了通信瓶颈。对于这个问题有两个技术:首先明确各个服务器的分工,也就是一看到某个URL就确定要某一台服务器去做(例如结尾数字为1的URL都要服务器1去下载),这样就可以避免重复下载,在明确分工的基础上,判断URL就可以批处理了,比如每次向Hash Table发送一大批询问,或者每次更新一大批Hash Table的内容。这样通信的次数就大大减少了。
书中没有提到具体的Hash Table存储的解决方案,个人理解可能参考参数服务器的分布式存储构架进行存储。
⑦搜索引擎的排序-网页质量度量与相关性度量
搜索引擎中,根据索引返回的网页数有成千上万条,那么该如何排序,把用户最想看到的结果排在前面呢。总的来讲,排名取决于两个信息:网页的质量信息(Quality),以及这个查询与每个网页的相关性信息(Relevance)。
网页质量的衡量
最初,一些衡量网络质量的方法或多或少地用到了指向某个网页的链接以及链接上的文本(在搜索技术中成为锚文本,Anchor Text)。真正找到计算网页自身质量的完美的数学模型的是Google创始人拉里·佩奇和谢尔盖·布林。PageRank的高明之处在于把整个互联网当作一个整体来对待,这无意中符合了系统论的观点。核心思想是,如果一个网页被很多其他网页链接,说明它受到普遍的承认和信赖,那么它的排名就高。另外,PageRank也考虑了网页排名高的网站贡献的链接权重大这个因素。现在就出现了一个问题,计算搜索结果的网页排名过程中需要用到网页本身的排名,这不就是"先有鸡还是先有蛋"吗?破解这个怪圈的是布林,他把这个问题变成了一个 二维矩阵相乘的问题,并用迭代的方法解决了这个问题,他们先假定所有网页的排名是相同的,然后根据这个初始值,算出各个网页的第一次迭代排名,然后再根据第一次迭代排名算出第二次迭代排名。而且他们从理论上证明了,不论初始值如何选取,这种算法都能保证网页排名的估计值能收敛到排名的真实值,值得一提的是,这种算法不需要任何人工干预。理论的问题解决了,数量庞大的网页有带来了实际问题,十亿个网页时,这个二维矩阵就是一百亿亿个元素。这么大的矩阵相乘,计算量是非常大的。佩奇和布林利用稀疏矩阵的计算技巧,大大简化了计算量,并实现了这个网页排名算法。
Google早期,并行化是半自动的,这样更新一遍所有网页的周期很长。2003年,Google的工程师迪恩(Jeffrey Dean)和格麦瓦特(Sanjay Ghemawat)发明了二MapReduce(矩阵相乘很容易分解成许多小任务),PageRank的并行计算完全自动化了。
PageRank的计算方法,结果向量B,为一个$1 \times N$的向量,初始时为$B_0=(\cfrac{1}{N},\cfrac{1}{N},…,\cfrac{1}{N})$,A为$N \times N$的矩阵,其中值代表第n个网页指向第m个网页的链接数。通过公式$B_i = A \cdot B_{i-1}$进行迭代,可以证明$B_i$最终会收敛至$B=B \cdot A$,一般来讲,只要10次左右的迭代基本上就收敛了,即两次迭代的结果$B_i$和$B_{i-1}$之间的差异非常小。
由于网页之间链接的数量相比互联网的规模非常稀疏,因此需要对零概率或者小概率事件进行平滑处理。
$B_i = [\cfrac{α}{N} \cdot I + (1-α)A] \cdot B_{i-1}$
其中N是互联网网页的数量,α是一个(较小的)常数,I是单位矩阵
网页与查询的相关性度量
2007年,技术和算法的重要性依然高于数据,因此确定相关性主要依靠算法。但是今天,由于商业搜索引擎已经有了大量的用户点击数据,因此,对搜索相关性贡献最大的是根据用户对常见搜索点击网页的结果得到的概率模型。如今,影响搜索引擎质量的诸多因素,除了用户的点击数据之外,都可以归纳成下面四大因素:
1.完备的索引。俗话说,巧妇难为无米之炊,如果一个网页不在索引中,那么再好的算法也找不到。
2.对网页质量的度量。当然现在看来,PageRank的作用比10年前已经小了很多。今天,对网页质量的衡量是全方位的,比如对网页内容权威性的衡量,一些八卦网站的PageRank可能很高,但是他们的内容权威性则很低。
3.用户偏好。一个好的搜索引擎会针对不同用户,对相同的搜索给出不同的排名。
4.确定一个网页和某个查询的相关性的方法。
TF-IDF
TF(Term Frequency 单文本词频),词频,关键词的出现次数/总字数。其中停止词,如“的”,“是”,“中”,的权重为0。对于一组关键词,可以得到$TF_1$,$TF_2$,…,$TF_n$
IDF(Inverse Document Frequency 逆文本频率指数),对于预测主题能力更强的词,权重越大,这个权重的衡量就是IDF,$log(\cfrac{D}{D_w})$,其中D为全部文本数,$D_w$为关键词w在$D_w$个文本中出现。即如果一个关键词只在很少的网页中出现,通过它就容易锁定搜索目标,它的权重也就应该大。其实,所谓IDF的概念就是一个特定条件下关键词的概率分布的交叉熵(KL散度),这样,关于信息检索相关性的度量,又回到了信息论。
现在,各家搜索引擎对关键词重要性的度量,都在TF-IDF的基础上做了一定的改进和微调,但是,原理上与TF-IDF相差不远。
⑧搜索引擎反作弊问题和搜索结果的权威性问题
搜索引擎反作弊
搜索引擎中排名靠前的网页不一定就是高质量的、相关的网页,而是商业味儿非常浓的作弊网页,它们采用不正当的手段(SPAM)提高自己网页的排名。
早期的作弊方法是重复关键词,有时为了不让读者看到过多讨厌的关键词,聪明一点的作弊者常用很小的字体或与背景相同的颜色来掩盖这些关键词,其实这种方法很容易被搜索引擎发现并纠正。有了PageRank后,就有了专门买卖链接的生意,有人会创建成百上千的网站用于链接客户的网页。但是大量地卖链接很容易露出马脚(流通量大后很容易找到源头)。当然,还会有各种各样其他的作弊手段,抓作弊是一种长期的“猫捉老鼠”的游戏。
作弊者所做的事情,就像是在手机信号中加入噪声,这种人为加入的噪声并不难消除,因为这些作弊方法不是随机的(否则就无法提高排名了),因此,可以在搜集一段时间的作弊信息后,将作弊者抓出来。即针对这些商业相关的搜索,采用一套“刚干扰”强的搜索算法。
首先,那些卖链接的网站,都有大量的出链(Out Links),而这些出链的余弦距离如果接近1,则说明这些网站间并无关系!那么很有可能这是一个卖链接的网站。其次,反作弊用到的另一个工具是图论。在图中,如果有几个节点两两互相都连接在一起,它们被称为一个Clique。作弊网站一般需要互相链接以提高自己的排名,图论中有专门发现Clique的方法,可以直接用于找到这些作弊网站的Clique。另外,至于术的方面,方法也很多,例如针对作弊的JavaScript跳转页面,通过解析相应JavaScript内容即可。
作弊的本质是在网页排名信号中加入了噪声,因此反作弊的关键是去噪声。沿着这个思路可以从根本上提高搜索算法抗作弊的能力,事半功倍,而如果只是根据作弊的具体特征头痛医头,脚痛医脚,则很容易被作弊者牵着鼻子走。
搜索结果的权威性
当用户问的是一些需要专业人士认真作答的的问题,比如医疗方面的问题,那么如何才能从众多信息源中找到最权威的信息,就成了近年来搜索引擎公司面对的难题。这些网页虽然权威性不高,但是文章常常写的很好看,名气也很大,PageRank也很高,但是它们的内容未必权威。其次,互联网上对同一个问题给出的答案常常互相矛盾。比如奥巴马的出生地,竟然有近百个答案,他的一些政敌说他生于肯尼亚,而官方给出的是夏威夷,虽然大家都知道政敌说的话未必可信,但是互联网又怎么知道谁是政敌呢?
这就会引出“权威性的度量”,为了引入这一点,我们引入一个概念“提及”(Mention),如果在各种新闻、学术论文或者其他网络信息页中,讨论到“吸烟危害”这一主题时,国际卫生组织和约翰·霍普金斯大学这两个组织作为信息源被多次提及,那么我们就有理由相信这两个组织是谈论“吸烟危害”这个主题的权威机构。需要指出的是,“提及”不像是超链接那样一目了然,它隐含在文章的自然语句中,需要通过自然语言处理的方式分析出来,即使有了好的算法,计算量也是非常大的。并且权威性与搜索主题是相关的,毕竟每个组织都只在自己的领域有权威性,使得存储量非常大,比如M个网页,N个搜索关键词时,我们要计算和存储$O(M \cdot N)$个结果,而一般的网页只需要M个结果。因此,只有在今天有了云计算和大数据技术的情况下,计算权威性才成为可能。
在计算权威度时,我们采用了句法分析、互信息和短语(词组)聚类这三种方法。
计算权威度的步骤:
1.对网站的文字进行句法分析,找到涉及主题的短语,以及对信息源的描述,这样大量的运算得益于皮耶尔领导开发的Google句法分析器足够快,而且有大量的服务器可供使用。
2.利用互信息,找到主题短语和信息源的相关性,即出现主题短语时更容易出现某些信息源。
3.对主题短语进行聚合,聚合那些字面上不同,但意义相同的主题短语,如“吸烟的危害”、“吸烟是否致癌”等等。这样我们就得到了一些搜索的主题。至于聚类的方法,可以采用前面提过的矩阵运算的方法。
4.对一个网站中的网页聚合,比如把一个网站下面的网页按照子域(Subdomain)或者子目录(Subdirectory)进行聚类。这一步的目的是,即使一个权威的网站,它下面的一些子域却未必具有权威性。比如约翰·霍普金斯大学的网站,它下面可能有很多子域的内容与医学无关。因此,权威性的度量只能建立在子域或者子目录这一级。
完成上述四个步骤后,我们就可以得到一个针对不同主题,哪些信息源(网站)具有权威性的关联矩阵。当然,在计算这个关联矩阵时,也可以像计算PageRank那样,对权威度高的网站给出“提及”关系更高的权重,并且通过迭代算法,得到收敛后的权威度关联矩阵。这样便可以在搜索结果中提升那些权威度高的信息源的结果,使得用户对搜索结果更放心。
⑨有限状态机和动态规划-地图与本地搜索的核心技术
2008年9月23日,Google、T-mobile和HTC宣布了第一款基于开源操作系统Android的3G智能手机,它可以利用全球卫星定位系统实现的全球导航功能。此时这个系统可以媲美任何一个卫星导航仪,加上他的地址识别技术(采用有限状态机)比卫星导航仪严格的地址匹配技术(不能输错一个字母)要好得多。智能手机的定位和导航功能,其实只有三项关键技术:第一,利用卫星定位,这一点传统的导航仪都能做到;第二,地址的识别;第三,根据用户输入的起点和终点,在地图上规划最短线路。
地址分析和有限状态机
地址的写法各种各样,且有比较复杂的上下有关的文法,例如 上海市北京东路XX号,南京市北京东路XX号,当识别器扫描到“北京东路”时,它和后面的门牌号能否构成一个正确的地址,取决于上下文,即城市名。在统计语言模型中有介绍,上下文有关的文法分析非常复杂又耗时,如果没有好的模型,这个分析器写出来很难看不说,很多情况无法覆盖。所幸的是,地址的文法是上下文有关文法中相对简单的一种,因此有许多识别和分析的方法,其中最有效的是有限状态机。有限状态机还能帮助google对用户输入的查询进行分析,挑出其中描述地址的部分,当然,剩下的关键词就是用户要找的内容。
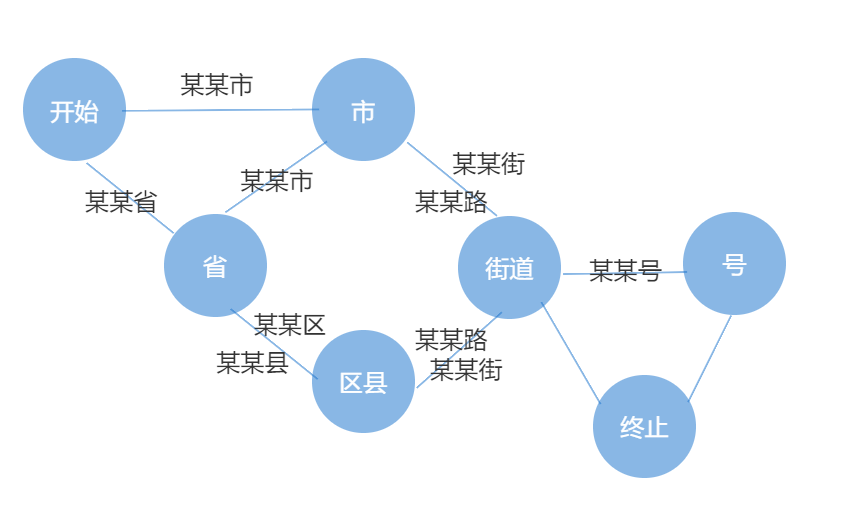
如果一个地址能从状态机的开始状态进过状态机的若干中间状态,走到终止状态,那么这条地址有效,否则无效。
使用有限状态机识别地址,关键要解决两个问题,首先,要通过给定地址建立状态机,然后,给定这个有限状态机后,地址字串的匹配算法。好在这两个问题都有现成的算法。
在实际情况中,用户输入地址不标准或有错别字时,有限状态机因为只能进行严格匹配,所以无法识别。其实,有限状态机在计算机科学早期的成功主要用于程序语言编译器的设计中。为了实现可以模糊匹配,基于概率的有限状态机被提出,它可以给出一个字串为地址的可能性,原理与离散的马尔科夫链基本等效。
值得一提的是,有限状态机的用途远不止于对地址这样的状态序列进行分析,在Google新一代的产品中,有限状态机被应用在Google Now,一个在智能手机上的基于个人信息的服务软件。他会根据个人的地理位置信息、日历和一些其他信息(对应于有限状态机里面的状态),以及用户当前语音或者文字输入,回答个人的问题,提供用户查找的信息,或者提供相应服务(如打开地图导航、拨打电话等)。Google Now的引擎和AT&T的有限状态机工具库从功能上讲完全等价。
有一些领域使用一种特殊的有限状态机——加权的有限状态机(Weighted Finite State Transducer, WFST),有限状态传感器的特殊性在于,每一个状态由输入和输出符号定义,任何一个词的二元组,都可以对应到WFST的一个状态,WFST是天然的自然语言处理的分析和解码工具。在语音识别中,每个句子都可以用一个WFST表示,WFST中的每一条路径就是一个备选句子,其中概率最大的那条路径就是这个句子的识别结果。而这个算法的原理是动态规划。
全球导航和动态规划
所有的导航系统都采用了动态规划(Dynamic Programming, DP)的办法,关于动态规划的思想及实现相信在数据结构及算法中已经讲解的很深刻,我在这里根据我在路径规划的研究和工作实践,补充一些其他经验。
路径规划问题的精确解,都会采用动态规划。而在一些节点数庞大,又对完全精确解需求不高的情况下,解决这种NP-hard问题运筹学中的启发式算法,近年来有很多强化学习被应用在路径规划中,但是由于强化学习的加入带来了时间成本的增加,算法整体效率并没有太大提升。
⑩余弦定理和新闻分类
所谓新闻的分类,或者更广义地讲文本的分类,无非是要把相似的新闻归入同一类中。这就要求我们先把文字的新闻变成一组可计算的数字,然后再设计一个算法来算出任意两篇新闻的相似性。
一个新闻可以用一个向量表示,根据TF-IDF,对其中的每一个词在词典中进行标识,例如一个65535个词的词典,那么就会形成一个65535维的向量,称为新闻的特征向量(Feature Vector)。和计算搜索相关性一样,出现在文本不同位置的词再分类时的重要性也不相同,一般,标题>正文开头结尾>正文中间。可以对标题和重要位置的词进行额外加权,以提高文本分类的准确性。
现在我们有了向量来代表一个新闻的内容,可以发现,同一类新闻用词一定是相似的。因此,可以通过计算两个向量的夹角来判断对应的新闻主题的接近程度,即余弦相似度。
$cosθ = \cfrac{<b,c>}{|b| \cdot |c|} = \cfrac{x_1y_1+x_2y_2+…+x_{65535}y_{65535}}{\sqrt{x_1^2+x_2^2+…+x_{65535}^2} \cdot \sqrt{y_1^2+y_2^2+…+y_{65535}^2}}$
在工程中,为了简化余弦相似度的计算复杂度$O(N^2·|a|)$,有以下三种方向,首先,分母部分(向量的长度)不需要重复计算,计算向量a和向量b的余弦时,可以先将它们的长度存起来,等计算向量a和向量c的余弦时,直接取用a的长度即可;其次,在计算分子,即两个向量内积时,只需考虑向量中的非零元素,如果一篇新闻有2000个词,那么非零元素一般只有1000个,这样计算的复杂度可以下降1000/词典总词数,计算时间直接从“天”下降到十几分钟这个量级;第三,可以删除虚词,进一步减少非零元素个数,另外删除虚词,不仅可以提高计算速度,对新闻分类的准确性也大有好处,因为虚词的权重其实是一种噪声。经过这些操作,10万篇新闻两两比较,计算时间也就几分钟而已,如果做几十次迭代,可以在一天内计算完。
具体的分类算法分为两种情形,第一种,假定我们已经有了已知每一类的特征向量,新的新闻特征向量就可以通过计算它与各类新闻特征向量的余弦相似度,来决定将它划分到哪一类中去。第二种,当我们是类似层次聚类,从第向上,一步一步合并直至类别越累越少,而每个类越来越大,当某一类太大时,这一类里一些新闻之间的相似性就很小了,这是就要停止迭代,这就是自动分类的方法。
本章介绍的这种新闻归类的方法,准确性好,适用于被分类的文本集合再百万数量级。如果大到亿这个数量级,那么计算时间还是比较长的。对于更大规模的文本处理,将在下一章介绍一种更快速但相对粗糙的方法。
⑪矩阵运算和文本处理中的两个分类问题
自然语言处理中,最常见的两个分类问题分别是,将文本按主题归类(比如新闻分类)和将词汇表中的字词按意思归类(比如将各种运动的项目名称都归到体育类)。这两个分类问题都可以通过矩阵运算来圆满地、一次性地解决。
上一章中的文本分类其实是一个聚类问题,关键是计算两篇新闻(向量)的相似度。运用余弦相似度时需要两两计算并且多次迭代,虽然算法漂亮但耗时长。我们希望有一个办法,一次就能把所有新闻相关性计算出来。这个一步到位的方法利用的是矩阵运算中的奇异值分解(Singular Value Decomposition, SVD)。
$M = UΣV$ $$ M=\left[ \begin{matrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1N} \ \cdots&&&&\cdots \a_{i1} & \cdots&a_{ij} & \cdots & a_{iN} \ \cdots&&&&\cdots\ a_{M1} & \cdots&a_{Mj} & \cdots & a_{MN} \ \end{matrix} \right] $$ 其中,每一行对应一篇文章,每一列对应一个词,如果有N个词,M篇文章,则得到一个$M \times N$的矩阵,第i行、第j列的元素$a_{ij}$,是字典中第j个词在第i篇文章中出现的加权词频(比如TF-IDF值)。
奇异值分解,就是把M,分解成三个小矩阵相乘。这三个矩阵有非常清晰的物理含义。
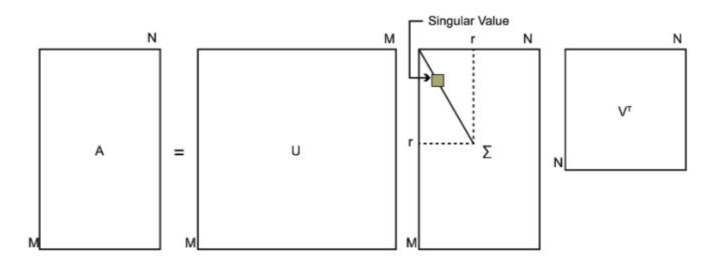
由于对角矩阵B对角线上的元素的很多值相对其他的值非常小,或者干脆为0,故可以省略。
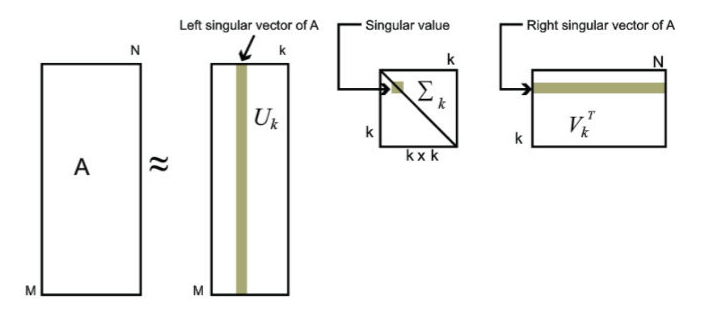
$U$的每一行表示一个词,每一列表示一个语义相近的词类,或者称为语义类,数值越大越相关。
$V$是对文本的分类结果,它的每一列对应一篇文本,每一行对应一个主题。这一列中的每个元素表示这篇文本在不同主题中的相关性。
$Σ$表示词的类和文章的类之间的相关性。
因此只要完成对关联矩阵$M$进行一次奇异值分解,就可以同时完成近义词分类和文章的分类。另外,还能得到每个主题和每个词的语义类之间的相关性。这个结果非常漂亮!
奇异值分解一般分为两步。首先,将矩阵A变成一个双对角矩阵,这个过程的计算量是$O(MN^2)$,当然这里假设M>N。我们仍然可以利用矩阵$A$的稀疏性大大缩短计算时间。第二步是将双对角矩阵变成奇异值分解的三个矩阵,这一步的计算量只是第一步的零头,可以忽略不计。在文本分类中,$M$对应文本的数量,$N$对应词典大小。奇异值分解的计算复杂度与余弦定理一次迭代的时间复杂度处于一个量级,但是它不需要多次迭代。奇异值分解的另一个大问题是存储量较大,因为整个矩阵都需要存在内存里,而利用余弦定理的聚类则不需要。实际应用中,可以先进行奇异值分解,得到粗分类结果,再利用计算余弦向量的方法,在粗分类的基础上,进行几次迭代,得到比较精确的结果。
理论的问题解决了,下面就是工程的实际问题,怎么利用计算机进行奇异值分解。这时,线性代数中的许多概念,比如矩阵的特征值,以及数值分析的各种算法等就统统派上用场了。对于不大的矩阵,比如几万乘几万的矩阵,用计算机上的数学工具MATLAB就可以计算。但是更大的矩阵,比如上百万乘上百万,奇异值分解的计算量非常大。虽然Google早就有了MapReduce等并行计算工具,但是由于奇异值分解很难拆成不相关的子运算,即使在Google内部以前也无法利用并行计算的优势来进行矩阵分解。直到2007年,Google中国(谷歌)的张智威博士带领几个中国的工程师及实习生实现了奇异值分解的并行算法,这是Google中国对世界的一个贡献。
⑫信息指纹及其应用
所谓信息指纹,可以简单理解为一段信息(文字、图片、音频、视频等)随机地映射到一个多维二进制空间中的一个点(一个二进制数字)。只要这个随机函数做得足够好,那么不同信息对应的这些点就不会重合,因此,这些二进制的数字就成了原来的信息所具有的独一无二的指纹。
字符串的信息指纹的计算方法一般分为两步,首先,把这个字符串看成是一个特殊、很长的整数,这一步非常容易,因为在计算机里本来就是这样存储的。接下来就需要用到一个产生信息指纹的关键算法:伪随机数产生器算法(Pseudo-Random Number Generator, PRNG),通过它把任意很长的整数转换成定长的伪随机数,现在常用的算法是梅森旋转算法(Mersenne Twister)。
另外,信息指纹的不可逆性为网络加密传输提供了很好的支持。一些网站会将用户访问的cookie(本来已经加密,但是如果某一访问所有网站的cookie都一样还是会暴漏行为)通过HTTPS加密。加密的可靠性,取决于是否很难人为地找到具有某一指纹的信息,即解密。从加密的角度来讲,梅森旋转算法还不够好,因为它产生的随机数还有一定的相关性,破解一个就等于破解了一大批。
在互联网上加密要使用基于加密的伪随机数产生器(Cryptographically Secure Pseudo-Random Number Generator, GSPRNG)。常用的算法有MD5或SHA-1等标准,它们可以将不定长的信息变成定长的128位或160位的二进制随机数。
除了上述信息指纹可以帮助快速且高效得判断文本相同和互联网加密外,信息指纹在互联网和自然语言处理中还有很多应用。
集合相同的判定
普通的先将两个集合排序,再进行比较的算法时间复杂度为$O(NlogN)$。或者将第一个表放在哈希表里,再用第二个表比对,这个方法可以达到最佳的$O(N)$时间复杂度,但是额外使用了$O(N)$空间,而且代码复杂。完美的办法是计算这两个集合中元素的指纹和,然后进行比较,加法的交换率,保证了集合的指纹不因元素次序变化而变化。类似如检测网络上某首歌曲是否盗版别人,只需要计算这两个音频的信息指纹即可。
判定基本相同
判定两个邮箱群发的接收电子邮件地址清单(Email Address List)是否相同,可以用来判断是否群发垃圾邮件。但是如果其中有一点小小的不同,上述信息指纹甚至会产生很大的不同。这个时候可以按照规则,挑选几组电子邮箱地址集,例如尾数为24的地址集与尾数为34的地址集,由于挑选的地址集数量一般为个位数,因此可以得到80%,90%重复这样的结果。又或者对网页中的,刨除常见词如“的”,“是”与只出现一次的噪声词,只需要找出剩下的词中IDF值最大的几个词,并且算出它们的信息指纹即可,为了允许有一定的容错能力,Google采用了一种特定的信息指纹——相似哈希(SimHash)。
假定一个网页中有若干词$t_1,t_2,…,t_k$,它们的权重(如TF-IDF)为$w_1,w_2,…,w_k$。先计算出这些词的信息指纹(假定有8位)。第一步扩展,如$t_1$的信息指纹为10100110,那么对$t_1$的权重$w_1$,逢1相加,逢0相减。这样在k次加减$w$之后,可以获得8个实数值。第二步收缩,这些实数值正数变1,负数变0,就可以重新获得一个8位的二进制数,这个数就是这个网站的SimHash。相似哈希的特点是,相同网页或只有小权重词不同网页的相似哈希必定相同,如果两个网页的相似哈希不同但相差很小,则对应的网页也非常相似。工程上使用的64位相似哈希,如果只差一两位,那么对应网页内容重复的可能性大于80%。
⑬密码学的数学原理
加密函数不应该通过几个自变量和函数值就能推出函数本身,这样一来,破译一篇密文就可能破译以后全部的密文。
香农提出的信息论为密码学的发展提供了理论基础,根据信息论,密码的最高境界是敌方在解惑密码后,信息量没有增加。一般来讲,当密码之间均匀分布且统计独立时,提供的信息量最少。均匀分布使地方无从统计,而统计独立可保证敌人即使知道了加密算法,并且看到了一段密码和明码后,无法破解另一段密码。
Diffie和Hellman在1976年的开创性论文“密码学的新方向”($\it{New \ Directions \ in \ Cryptography}$),介绍了公钥和电子签名的方法,这是今天大多数互联网安全协议的基础。
虽然公开密钥下面有许多不同的具体加密方法,比如早期的RSA算法、Rabin算法、和后来的ElGamal算法、椭圆曲线算法(Elliptic curve),它们的原理基本一致,并不复杂:
1.它们都有完全不同的密钥,一个用于加密,一个用于解密
2.这两个看上去无关的密钥,在数学上是关联的
以下是一个公开密钥的原理:
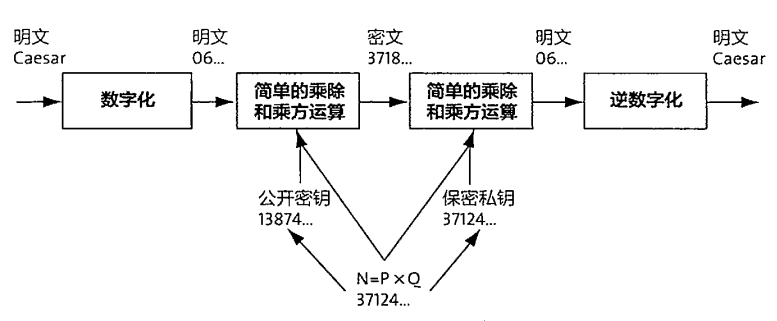
公开密钥的好处:
1.简单,就是一些乘除而已。
2.可靠,公开密钥方法保证产生的密文是统计独立而分布均匀的。也就是说,不论给出多少份明文与密文的对应,也无法破解下一份密文。更重要的是N、E可以公开给任何人进行加密,但是只有掌握私钥D的人才可以解密,即使加密者也是无法破解的。
3.灵活,可以产生很多的公开密钥E和私钥D的组合给不同的加密者。
最后让我们看看破解这种密码的难度。至今的研究结果表明最彻底的方法还是对大数N进行因数分解,即通过N反过来找到P和Q,这样密码就被破解了。而找到P和Q目前只有一个方法:用计算机把所有可能的数字试一遍,这实际上实在拼计算机的速度,这也就是为什么P和Q都需要非常大。一种加密方法只要保证50年内计算机破解不了,也就算是令人满意了。
遗憾的是,虽然在原理上非常可靠,但是很多加密系统在工程实现上却留下了不少漏洞。因此,很多攻击者从攻击算法转而攻击实现方法。
⑭数学模型的重要性
1.一个正确的数学模型应当在形式上是简单的
2.一个正确的模型一开始可能还不如一个精雕细琢过的错误模型来的准确,但是,如果我们认定大方向是对的,就应该坚持下去
3.大量准确的数据对研发很重要
4.正确的模型也可能受噪声干扰,而显得不准确;这时不应该用一种凑合的修正方法加以弥补,而是要找到噪声的根源,这也许能通往重大的发现
⑮最大熵模型
当需要综合几十甚至上百种不同的信息,最大熵模型可以保留全部的不确定性(除了已知的信息,不做主管假设),将风险降到最小。最初,计算能力还不足时,只能处理计算量相对不太大的自然语言处理问题,拉纳帕体成功将上下文信息、词性(名词、动词和形容词)以及主谓宾等句子成分,通过最大熵模型结合起来,做出了当时世界上最好的词性标识系统和句法分析器。且至今仍然是使用单一方法的系统中效果最好的。在2000年前后,计算机速度的提升以及训练算法的改进,很多复杂的问题,包括句法分析、语言模型和机器翻译都可以采用最大熵模型了。最大熵模型和一些简单组合了特征的模型相比,效果可以提升几个百分点,对于投资这种很少的提升也能带来巨大的利润的行业来说非常有效,所以很多对冲基金开始使用最大熵模型。
$P(d|x_1,x_2,…,x_{20}) = \cfrac{1}{Z(x_1,x_2,…,x_{20})} e^{λ_1(x_1,d)+λ_2(x_2,d)+…+λ_{20}(x_{20},d)}$
其中,归一化因子为:
$Z(x_1,x_2,…,x_{20}) = \sum\limits_{d}e^{λ_1(x_1,d)+λ_2(x_2,d)+…+λ_{20}(x_{20},d)}$
在实现方法上,从GIS(Generalized Iterative Scaling)到IIS(Improved Iterative Scaling)缩短了一到两个数量级,再到吴军找到的数学变换在IIS的基础上减少两个数量级,再加上现代的MapReduce并行计算,现在,再1000台计算机上并行计算一天就可以完成了。
逻辑回归损失函数的基于伯努利分布的最大似然法,与交叉熵损失函数本质相同(经过log变换后公式相同),可见信息论的思想,变换无穷但又不离本质。
⑯拼音输入法的数学原理
输入汉字的快慢取决于汉字编码的平均长度诚意寻找这个键所需的时间。单纯地编短编码长度未必能提高输入速度,因为寻找一个键的时间可能变得很长。
对汉字的编码分为两部分:对拼音的编码和消除歧义性的编码。早期的输入法常常只注重第一部分而忽视第二部分,中国最早的汉字输入微机中华学习机和长城0520采用的都是双拼,即每个字母代表一个或多个声母或韵母,这种输入方法看似节省了编码长度,但是输入一点也不快,一是因为增加了歧义性(很多韵母不得不共享一个字母键),二是双拼比按照拼音的全拼增加了拆字的过程,三是容错性不高,比如an,ang的编码完全没有相似性,一个好的输入法不能要求用户读准每个字的发音。早期的输入法都是这样,一味的追求更少的输入的编码(当然它们都声称自己的编码比其他的输入法更合理,但从信息论的角度上看都是一个水平线上的),而忽视了找到每个键所用的时间,要求普通用户背下这些输入方法里所有汉字的编码是不现实的。
最终,用户还是选择了拼音输入法。它不需要专门学习,并且输入自然,即找每个键的时间很短,另外因为编码长,有信息冗余,容错性好。于是,拼音输入法要解决的问题只剩下排除一音多字的歧义性了,这也是目前各种拼音输入法的主要工作。接下来我们就分析平均输入一个汉字可以做到最少几次击键。
按照香农第一定理,对于一个信息,任何编码的长度都不小于它的信息熵。以GB2312,6700个常见字集计算,汉字的信息熵在10个比特以内,如果假定输入法只能用26个字母,那么每个字母可以代表log26≈4.7bit($2^{4.7}≈26$),也就是输入一个汉字平均需要敲10/4.7≈2.1次键盘。而如果把汉字组成词,再以词为单位统计信息熵,不考虑上下文相关性,那么每个汉字的平均信息熵就会减少为8bit,这也是现在所有输入法都基于词输入的根本原因。如果再考虑上下文相关,可以将每个汉字的信息熵降到6bit,这是输入一个汉字只需要敲6/4.7≈1.3次键盘。但事实上没有一种输入法能接近这个效率,有两个原因,首先,需要根据词频进行特殊编码,而上一段说过特殊编码会增加找到每个键的思考时间,其次上,在个人电脑上,很难安装非常大的语言模型。
事实上,现在汉语全拼的平均长度为2.98,如果能利用上下文解决一音多字的问题,全拼输入法的平均击键次数应该小于3次。而解决上下文问题,10年前的拼音输入法(以紫光为代表)解决这个问题的办法是建立大词库,但是这种方法多少根据经验和直觉,一直是在打补丁。而利用上下文最好的方法是借助语言模型,目前,各家输入法(Google、腾讯和搜狗)基本处在同一个量级,将来技术上进一步提升的关键在于看谁能准确而有效地建立语言模型。
拼音转汉字的算法和在导航中寻找最短路径的算法相同,都是动态规划。
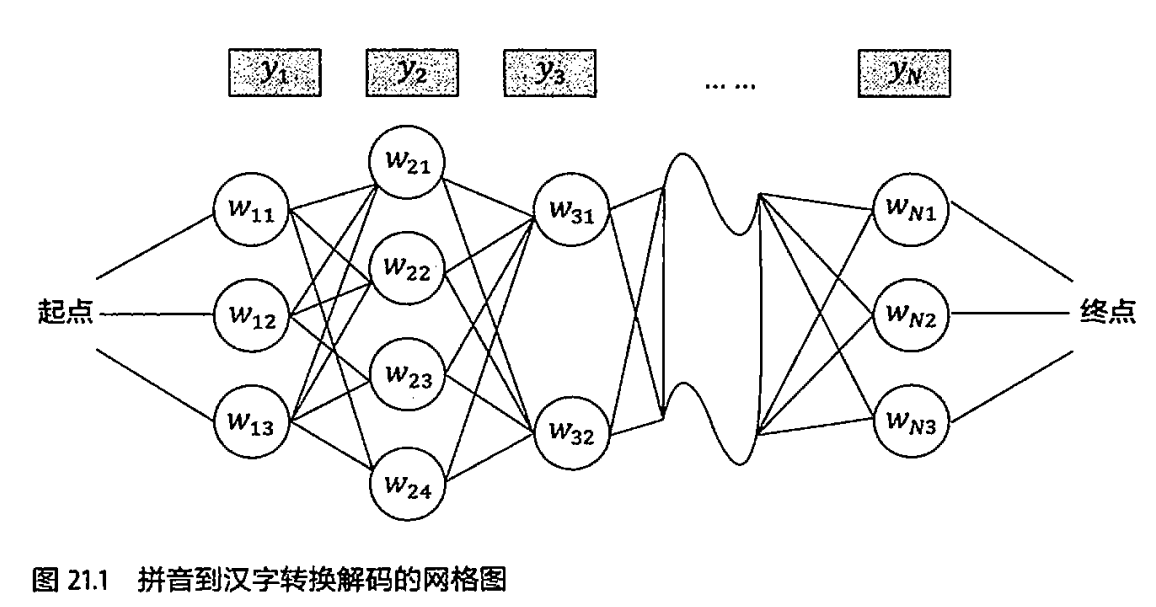
每一条路,都是一个可选结果,找到概率最高的一条就是最优的句子:
$w_1,w_2,…,w_N = \mathop{ArgMax}\limits_{w∈W}P(W_1,W_2,…,w_n|y_1,y_2,…,y_N)$
上述公式的简化方法:
$w_1,w_2,…,w_N = \mathop{ArgMax}\limits_{w∈W}P(y_1,y_2,…,y_N|W_1,W_2,…,w_n)\ \cdot \ P(W_1,W_2,…,w_n)≈ \mathop{ArgMax}\limits_{w∈W}\prod\limits_{i=1}^{N}P(w_i|w_{i-1})·P(y_i|w_i)$
如果对上述简化公式中的概率取对数同时取反,即定义$d(W_{i-1},W_i)=-logP(w_i|w_{i-1})·P(y_i|w_i)$,上面的连乘关系,就变成了加法关系,寻找最大概率的问题,就变成了最短路径问题。
当输入速度超过一定阈值后,用户的体验可能更重要,客户端上虽然不能放置太大的语言模型,但是可以建立个性化的语言模型。那么就有两个问题:如何训练一个个性化的语言模型,其次是怎样处理好它和通用语言模型的关系。为某个人训练一个特定的词汇量在几万的二元语言模型需要几千万的语料,这对一个人来说可能一辈子也达不到,没有足够多的训练数据,高阶的语言模型根本没用,一些输入法就找到了一种经验做法:用户词典,这实际上是一个小规模的一元模型加上非常小量的元组(比如一个用户定义的词ABC,实际是一个三元组)。
更好的办法是找到大量符合用户经常输入的内容和用语习惯的语料,训练一个用户特定的语言模型。这就要用到余弦定理和文本分类的技术了,即找到某个人输入文本的特征向量Y和已有文本$X_1,X_2,…,X_{1000}$,选择前K个和Y距离最近的类对应的文本,作为这个特定用户语言模型的训练数据。
大部分情况下,$M_1$对这个特定用户的输入比通用模型$M_0$好,但是对于相对冷僻的内容,$M_1$的效果就远不如$M_0$了,所以我们需要综合两个模型。把各种特征综合在一起的最好方法是采用最大熵模型,当然,如果为每个人都建立这样一个模型,成本较高。因此可以采用一个简化的模型:线性插值模型,能得到最大熵模型约80%的收益,Google拼音输入法的个性化语言模型就是这么实现的。
⑰布隆过滤器
判断一个元素是否在一个集合中,按12章信息指纹所描述的,可以通过8个字节的信息指纹哈希表,但由于哈希表的存储效率一般只有50%,因此一个元素需要占用16个字节,一亿个地址大约要1.6GB,即16亿字节的内容,那么存储几十亿个邮件地址需要上百GB,除非是超级计算机,一般服务器是存不下的。
而我们现在介绍的一种称作布隆过滤器的数学工具,它只需要哈希表$\cfrac{1}{8}$到$\cfrac{1}{4}$的大小就能解决同样的问题。布隆过滤器(Bloom Filter)是由伯顿·布隆(Burton Bloom)于1970年提出的,它实际上是一个很长的二进制向量和一系列随机映射函数。
假定存储一个亿个电子邮件,那么我们使用16亿个比特位,每个比特位初始值为0。对于每个电子邮件地址X,用8个不同的随机数产生器($F_1,F_2,…,F_8$)产生8个信息指纹,再用一个随机数产生器G把这8个信息指纹映射到1-16亿中的8个自然数$g_1,g_2,…,g_8$。然后把这8个位置的比特位全部设置为1。在把所有邮件都处理后,一个针对这些电子邮件的布隆过滤器就建成了。当有一个新的电子邮件地址Y时,就将Y重复上述的处理结果,然后检查这8个位置是否都是1就行了。当然根据这个逻辑,布隆过滤器决不会漏掉任何一个可以地址,但是,当某个好的电子邮件对应的8个位置都恰好被设置成1时,就会被误判为黑地址。好在这种可能性很小,对于一个元素的集合,这种误识别率在万分之一以下。常见的补救方法是建立一个小的白名单,存储那些可能被误判的地址。
误判率的计算,先计算某个比特被设为1个概率,根据伯努利分布,$1-(1-\cfrac{1}{m})^{kn}$。而对于一个新的不在集合中的元素,它的k个bit每个都命中的概率为$(1-(1-\cfrac{1}{m})^{kn})^{k}$,化简后为
$P = (1-e^{-\cfrac{ln{(\cfrac{m}{n}ln2)n}}{m}})^{ln(\cfrac{m}{n}ln2)}$
如果n比较大,可以近似为
$(1-e^{-k(n+0.5)/(m-1)})^k ≈ (1-e^{\cfrac{kn}{m}})^k$
假定一个元素用16bit,即k=8,那么假阳性的概率为万分之五。当然这根据m(布隆过滤器的总bit),n(集合中元素数),k(判定一个元素使用的bit数)的不同有所差别。根据直觉,m越大误判率越小,n越大误判率越大,而k从1开始误判率会经过一个先减小再增加的过程。
⑱马尔可夫"网络"——贝叶斯网络
马尔可夫链描述了一种状态序列,其每一个状态值取决于前面有限个状态,但实际问题中,很多事物相互的关系并不能用一条链串起来,很可能是交叉的、错综复杂的,如图:
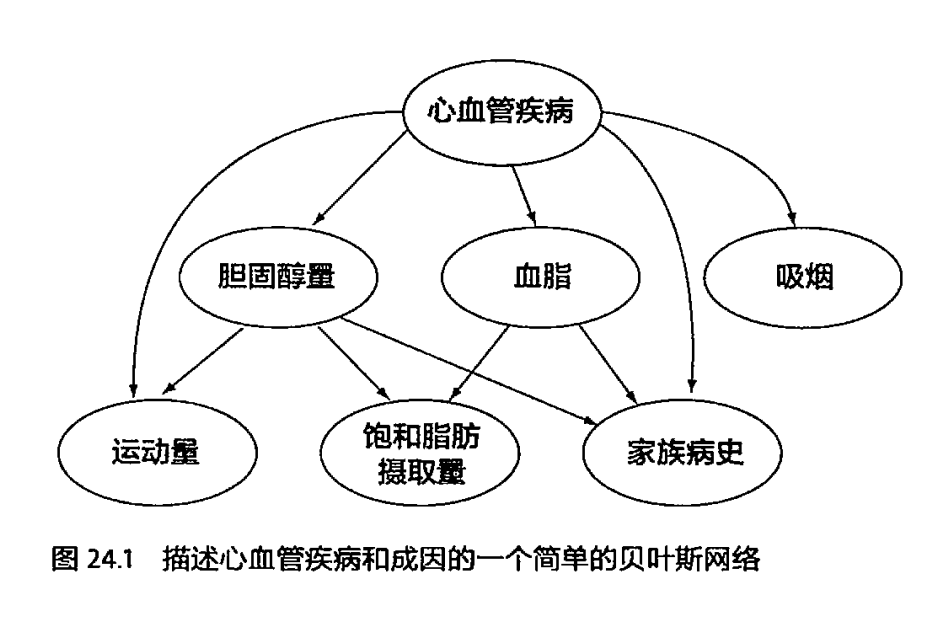
每一个edge都表示一个量化的可信度(belief),马尔可夫假设保证了贝叶斯网络便于计算,在网络中,每个节点的概率,都可以用贝叶斯公式来计算,贝叶斯网络因此得名,又因为每个edge都有一个可信度,贝叶斯网络也被称作信念网络(Belief Networks)。
使用贝叶斯网络必须先确定这个网络的拓扑结构,然后还要知道各个状态之间相关的概率,得到拓扑结构和这些参数的过程分别叫做结构训练和参数训练,统称训练。和训练马尔可夫模型一样,训练贝叶斯网络要用一些已知的数据,并且贝叶斯网络的训练比较复杂,从理论上讲,它是一个NP-hard问题。但是对于某些应用,这个训练过程可以简化,并在计算机上实现。
优化的贝叶斯网络要保证它产生的序列从头走到尾的可能性最大,即后验概率最大。当然产生一个序列可以有多条路径,从理论上讲,需要完备的穷举搜索(Exhaustive Search),但这就是Np-Hard的了,因此一般采用贪心算法(Greedy Algorithm),也就是在每一步时,沿着箭头的方法寻找有限步,为了防止陷入局部最优,可以采用蒙特卡洛(Monte Carlo),用许多随机数在贝叶斯网络中试一试,看看是否陷入局部最优,这个方法计算量比较大。最近,新的方法是利用信息论,计算节点之间两两的互信息,只保留互信息较大的节点直接的连接,然后再对简化了的网络进行完备的搜索,找到全局优化的结构。
找到结构后就要对参数进行训练了,假定这些权重用条件概率来度量,我们需要优化贝叶斯网络的参数,使得观察到的这些数据的概率(即后验概率)$P(D|θ)$达到最大,这个过程就是EM过程。在计算后验概率时,计算的是条件X和结果Y之间的联合概率$P(X,Y)$,我们的训练数据会提供一些$P(X,Y)$之间的限制条件,而训练出来的模型要满足这些条件。并且这个模型应该是满足最大熵模型的,因此涉及最大熵模型的训练方法在这里都能使用。
值得一提的是,结构的训练和参数的额训练通常是交替进行的。IBM华生实验室的茨威格博士(Geoffrey Zweig)和西雅图华盛顿大学的比尔默教授(Jeff Bilmer)完成了一个通用的贝叶斯网络的工具包,提供给贝叶斯网络有兴趣的研究者免费使用。
贝叶斯网络再图像处理、文字处理、支持决策等方面有很多应用。在文字处理方面,语义相近的词之间的关系可以用一个贝叶斯网络来描述,我们利用贝叶斯网络,可以找出近义词和相关的词,因而在Google搜索和Google广告中都有直接的应用。
贝叶斯网络可用于分析文本,抽取概念,分析主题,这是一种主题模型(Topic Model)。前面提到的余弦相似性和奇异值分解方法都是主题模型的一种。这里介绍通过贝叶斯网络建立的另一种模型——Google的Rephil。在主题模型中,一个主题可以包含多个词,一个词也可以属于多个主题,那么就可以用贝叶斯网络建立一个文章、概念和关键词之间的联系:
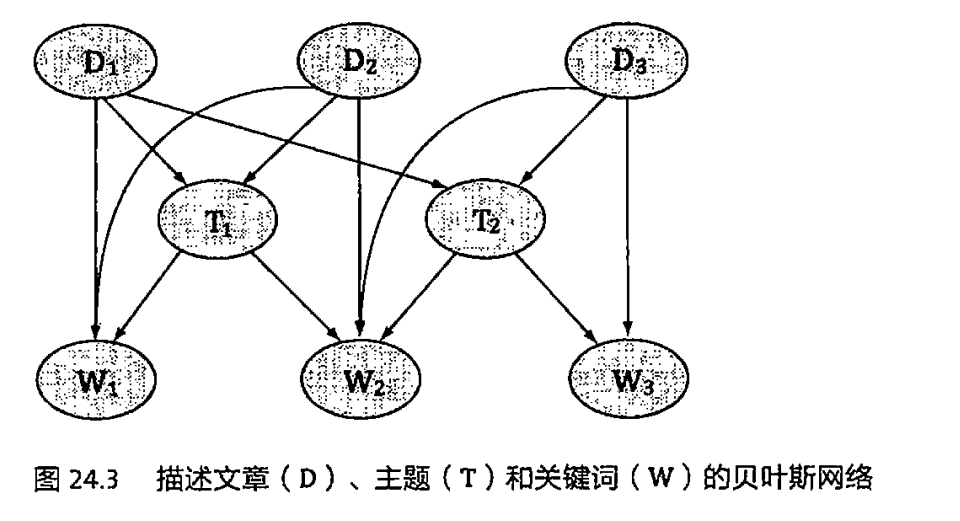
其中,文章和关键词本身有直接的关联,它们两者都还和概念有直接关联,同时它们通过主题还有间接的关联。
其他参考资料:
比尔默于茨威格共同发表的论文:http://people.ece.uw.edu/~bilmes/pgs/sort_Date.html
斯坦福大学科勒(Daphne Koller)教授的巨著:$\it{Probabilistic \ Graphical \ Models \ :Principles \ and \ Techniques}$
⑲条件随机场、文法分析与其他
句法分析(Sentence Parsing),指根据文法对一个句子进行分析,建立这个句子的语法树,即句法分析(Syntactic Parsing)。20世纪80年代前,人们受形式语言学的影响,采用基于规则的方法,这种方法规则非常多,并且一旦某一步走岔了,需要回溯很多步,计算复杂度大的不得了。20世纪80年代后,布朗大学计算机系的计算语言学家尤金·查尼阿克(Eugene Charniack)统计出文法规则的概率,在选择文法规则时坚持一个原则——让被分析的句子的语法树概率达到最大。马库斯的学生拉纳帕提把文法分析看成是一个括括号的过程,每次从左到右扫描句子的每个词(或句子成分)时,只需要判断是否属于以下三个操作之一:
A1.是否开始一个新的左括号,比如在“美联储”是新括号的开始。
A2.是否继续留在这个括号中,比如在“保险公司”的位置,是否继续留在括号中。
A3.是否结束一个括号,即标上右括号,比如“资金”的位置是一个括号的结束。
为了判断采用哪个操作,拉纳帕提建立了一个统计模型$P(A|prefix)$,其中A表示行动,句子前缀$prefix$是指句子从开头到目前为止所有的词和语法成分。拉纳帕提用最大熵模型实现了这个模型,当然,拉纳帕提还用了一个统计模型来预测句子成分的种类。但是这种方法对于非常“规矩“的语句,分析正确率在80%以上,但是2000年后,随着互联网的普及,非严谨的句子中这个模型的正确率连50%也达不到,所幸在很多自然语言处理的应用中,并不需要对语句做深入的分析,只要做浅层的分析(Shallow Parsing),比如找出句子中主要的词语以及它们之间的关系即可。
到了20世纪90年代以后,随着计算机计算能力的增强,科学家们采用了一种新的数学模型工具——条件随机场,大大提高了句子浅层分析的正确率,可达到95%,使文法分析得以应用到很多产品,比如机器翻译上。
⑳维特比和他的维特比算法
维特比算法是一个特殊但应用最广的动态规划算法,维特比算法是针对一个特殊的图——篱笆网络(Lattice)的有向图最短路径问题而提出的。它之所以重要,是因为凡是使用隐马尔可夫模型描述的问题都可以用它来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
以输入法拼音转汉字为例,输入可见的序列$y_1,y_2,…,y_N$,而产生他们的隐含序列使$x_1,x_2,…,x_N$,$P(x_i|x_{i-1})$是状态之间的转移概率,$P(y_i|x_i)$是每个状态的产生概率。这个马尔可夫链的每个状态的输出是固定的,但是每个状态的值可以变化,比如输出读音”zhong“的字可以是”中“”钟“等多个字。
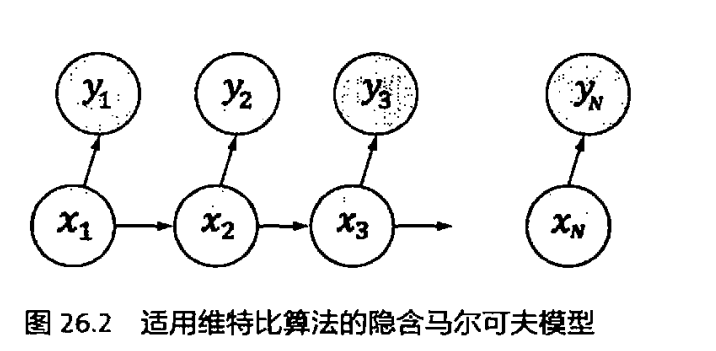
用符号$X_{ij}$表示状态$x_i$的第$j$个可能的值,如果把每个状态按照不同的值展开,就得到下图的篱笆网络
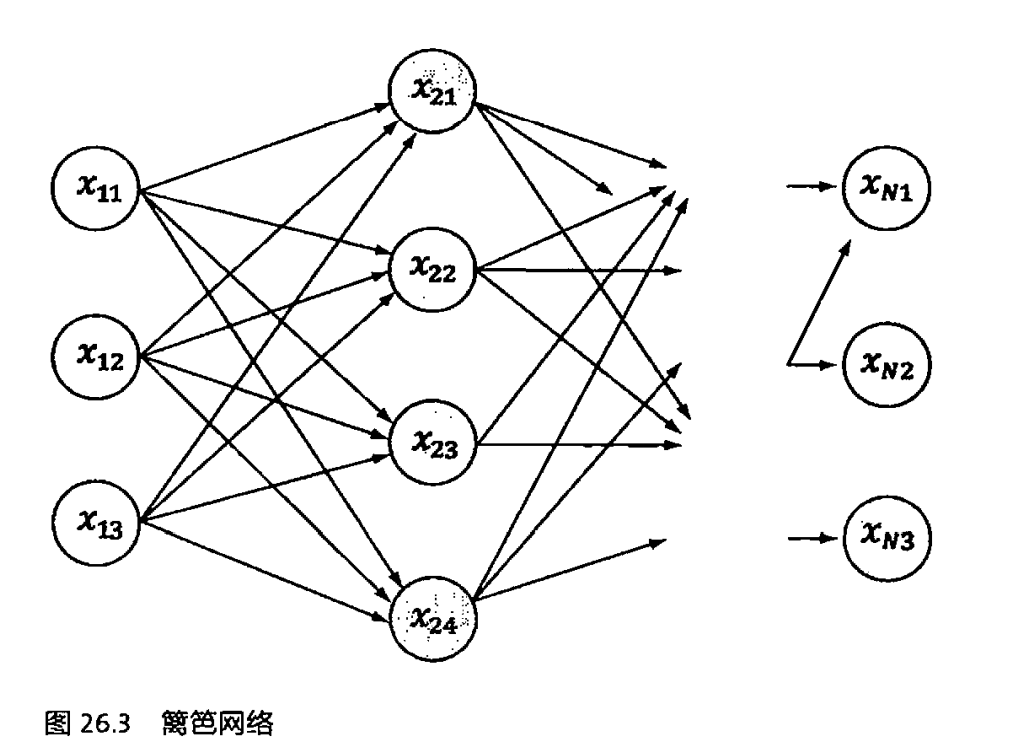
每一条路径都能产生我们观察到的输出序列Y,我们要找到的就是最可能(P最大)的一条路径。但是这样的路径组合数非常多,假定句长为10个字,那么这个组合数为$13^5~5 \times10^{14}$。假定计算每条路径需要20次乘法,就是$10^{16}$次计算,而今天的处理器每秒计算$10^{11}$次的话,也需要一天时间。因此需要一个最好能和状态数目成正比的算法,这就是维特比算法。
维特比算法的基础可以概括成以下三点:
1.如果概率最大的路径$P$(或者说最短路径)经过某个点,那么这条路径上从起始点$S$到这个点的子路径$Q$一定是$S$到这个点的最短距离,否则,用$S$到这个点的最短路径$R$替代$Q$,便构成了一条比P更短的路径,这显然是矛盾的
2.从$S$到$E$路径必定经过第$i$时刻的某个状态,即对于每个$x$,都要经过它的一个状态,不能跳过其中一个时刻。假定第$i$时刻有$k$个状态,那么如果记录了从$S$到第$i$个状态的所有$k$个节点的最短路径,那么最终的最短路径一定经过其中一条。这样,在任何时刻,只要考虑非常有限条候选路径即可
3.结合上述两点,假定当我们从状态$i$进入状态$i+1$时,从$S$到状态$i$上各个节点的最短路径已经找到,那么在计算从起点$S$到第$i+1$状态的某个节点的最短路径时,只要考虑从S到钱一个状态$i$所有的$k$个节点的最短路径,以及从这$k$个节点到$x_{i+1},j$的距离即可
基于上述三点基础,维特比算法过程如下:
step1.从S出发,对于第一个状态$x_1$的各个节点,不妨假定有$n_1$个,计算出$S$到它们的距离$d(S,x_{1i})$,其中$x_{1i}$代表任意状态1的节点。因为只有一步,所以这些距离都是S到它们各自的最短距离
step2.对于第二个状态$x_2$的所有节点,要计算出从S到它们的最短距离。路径长度$d(S,x_{2i}) = d(S,x_{1j})+d(x_{ij},x_{2i})$,由于$j$有$n_1$种可能,我们要一一计算,然后找到最小值,即
$d(S,x_{2i})=min_{I=1,n_1}d(S,x_{1j})+d(x_{1j},x_{2i})$
此时,第二个状态有多少个个节点(假设每个节点只有一条最短路径),就有多少个可能路径,与第一个状态的节点数就无关了,这样一直走到最后一个状态,就得到了整个网格从头到尾的最短路径,每一步计算的复杂度都和相邻两个状态$S_I$和$S_{i+1}$各自的节点数$n_i,n_{i+1}$成正比,即$O(n_i \cdot n_{i+1})$。如果假定在这个隐马尔可夫链中节点最多的状态有D个节点,也就是说整个网格的宽度为D,那么任何一步的复杂度不超过$O(D^2)$,由于网格长度是$N$,所以整个维特比算法的复杂度是$O(N \cdot D^2)$。回到上述那个输入法问题,计算量基本上是$13 \times 13 \times 10 = 1690≈10^3$,这和原来的$10^{16}$有天壤之别。更重要的是,维特比算法与长度$N$成正比,无论是在通信中,还是在语音识别、打字中,输入都是按照流(Stream)的方式进行的,制药处理每个状态的时间比讲话或者打字速度快(这点很容易做到),那么无论输入有多长,解码过程永远是实时的。
不知道有没有同学对这个算法的原理有非常似曾相识的感觉,其实这个算法与最短路径算法中的Dijkstra算法很相似——它们的基础理论是相似的,但是具体实现及应用场景有些许不同。首先,维特比只能用于有向无环图求最长最短路径,因为有环的时候 维特比的动态规划的递推公式会相互依赖形成类似于死锁的结构,没法解出来。其次,Dijkstra不适用于有负权值的场景。再次,Dijkstra是找一个节点到其他所有节点到最短路径,viterbi则是在篱笆网络里找一条从起点到终点(可能有多个起点,多个终点)的最短路径。HMM,CRF等算法中使用Viterbi算法,是因为Viterbi算法的效率比Dijsktra算法高。
㉑CDMA技术——3G移动通信的基础
最早,海蒂·拉玛尔(Hedy Lammarr)与她的邻居乔治·安泰尔(George Antheil)一道发明了一种称为”保密通信系统“的调频通信技术。这种传输方式是在一个较宽的扩展频带上进行的,因此它称为扩频传输(Spread-Spectrum Transmission)。和固定频率的传输相比,它有三点明显的好处:
1.它的抗干扰能力强。当有人想用噪音干扰固定的广播频率时,对于扩频传输来说基本不可能,因为不能把所有的频带都干扰了,否则整个国家的通信就中断了。
2.扩频传输的信号很难被截获。以极低的功率在很宽的频带上发送加密信号,对于试图截获者来讲,这些信号能量非常低,很难获取。
3.扩频传输利用带宽更充分。固定频率的通信由于邻近的频率相互干扰,载波频率的频点不能分布得太密集,两个频点之间的频带就浪费了。扩频通信由于抗干扰能力强,浪费的频带较少。
虽然这种扩频技术和调频技术早在20世纪60年代就应用于军事,但是转为民用则是20世纪80年代以后的事情,在CDMA以前,移动通信使用过两种技术:频分多址(FDMA)和时分多址(TDMA)。
频分多址,是对频率进行切分,每一路通信使用一个不同的频率,对讲机采用的就是这个原理。由于相邻频率会互相干扰,因此每个信道要有足够的带宽。如果用户数量增加,总带宽就必须增加。我们知道空中的频带资源是有限的,因此要么必须限制通信人数,要么降低话音质量。
时分多址是将同一频带按时间分成很多份。每个人的(语音)通信数量在压缩后只占用这个频带传输的$\cfrac{1}{N}$时间,这样同一个频带可以被多个人同时使用了。第二代移动通信的标准都是基于TMDA的。
前面讲了,扩频传输对频带的利用率比固定频率传输高,因此,如果把很多细分的频带合在一起,很多路信息同时传输,那么应该可以提高带宽的利用率。

由于每个发送者有不同的密码,接收者在接到不同信号时,通过密码过滤掉自己无法解码的信号,就可以避免相邻频率干扰的问题。由于这种方法是根据不同的密码区分发送的,因此称为码分多址(CDMA)。
㉒上帝的算法——期望最大化算法
在一般性问题中,如果有非常多的观测数据,定义一个最大化函数,经过若干次迭代,我们需要的模型就训练好了。这实在是太美妙了。
前面介绍过的很多算法,其实都是EM算法,比如隐马尔可夫模型的训练方法Baum-Welch算法,以及最大熵模型的训练方法GIS算法。在Baum-Welch算法中,E过程就是根据现有的模型计算每个状态之间转移的次数(可以是分数值)以及每个状态产生它们输出的次数,M过程就是根据这些次数重新估计隐马尔可夫的参数。这里最大化的目标函数就是观测值的概率。在最大熵模型的通用迭代算法GIS中,E过程就是跟着现有的模型计算每一个特征的数学期望值,M过程就是根据这些特征的数学期望值和实际观测值的比值,调整模型参数。这里,最大化的目标函数是熵函数。
值得一提的是,在凸函数中,EM算法一定能达到最优解,但是在非凸函数中,EM算法可能陷于局部最优解。
㉓逻辑回归和搜索广告
搜索广告基本上走过了三个阶段。第一个阶段以早期的Overture和百度的广告系统为代表,按广告主出价高低来排名。第二个阶段,Google按照预测哪个广告可能被点击,综合出价和点击率(Click Through Rate, CTR)等因素决定广告的投放。第三个阶段是进一步的全局优化。这章主要介绍第二阶段。
预估点击率有以下几点问题,首先,对于新广告的冷启动问题,第二,点击数据少,统计数据不足的问题,第三,广告的点击量显然与展示位置有关,因此,在预估点击率时,必须消除这些噪音。最后还要指出,影响点击率的因素非常多,这些都是在预估点击率时要考虑的。
需要整合这些特征,工业界普遍采用了逻辑回归模型(Logistic Regression Model)。逻辑回归作为最基础的广义线性模型,这里就不多介绍了。一个广告系统中,点击率预估机制的好坏决定了能否城北提高单位搜索的广告收入。而目前Google和腾讯的广告系统在预估点击率都采用了逻辑回归函数。
另外提一句,CTR在推荐中的实现,现在工业上会使用DeepFM、Wide&Deep等深度学习模型。
㉔分布式和Google云计算的基础
MapReduce实Google云计算的基础,将一个大任务拆分成小的子任务,并且完成了子任务的计算,这个过程叫做Map,将中间结果合并成最终结果,这个过程叫做Reduce。
㉕Google大脑和人工神经网络
无论是在计算机科学、通信、生物统计和医学,还是在金融和经济学(包括股市预测)中,大多数与“智能”有点关系的问题,都可以归结为一个在多维空间进行模式分类的问题。模式分类的任务就是要在空间里切一刀,将多个类分开,如语音识别中,就是把韵母a和e分开,有了深度学习,我们就可以实现特征工程自动化了。
除了神经元之间的线性关系之外,毕竟线性关系上的线性关系还是线性关系,并无意义,所以为了实现复杂的弯曲的世界,我们会增加非线性映射。为了通用性,一般在人工神经网络中,规定神经元函数只能对输入变量线性组合后的结果进行一次非线性变换。请注意是组合后的结果,将每一个输入值都进行非线性变换后再线性组合在一起是不被允许的(这样的计算量太大了)。
从理论上讲,人工神经网络只要设计得当,就可以实现任何复杂曲线(在高维空间里是曲面)的边界。
总的来说,人工神经网络是一个分层的有向图,第一层输入节点$X_1,X_2,…,X_n$接受输入的信息,也成为输入层。来自这些点的数值$x_1,x_2,…,x_n$按照它们输出的弧的权重($w_0,w_1,w_2,…,w_n$)进行加权,然后再做一次函数变换$f(G)$,赋给第二层的节点Y。
第二层的节点照此将数值向后传递,直到最后一层,最后一层又被称为输出层,输出层哪个节点的数值最大,输入的模式就被分在了哪一层。
在人工神经网络中,需要设计的部分只有两个,一个是它的结构,即网络分几层,每层几个节点,节点之间如何连接等等;第二就是非线性函数$f(·)$的设计,常用的函数有指数函数,sigmoid等,在指数函数时,它的模式分类能力等价于最大熵模型。
值得指出的是,如果我们把不同输出节点上得到的值看成是一种概率分布,那么实际上人工神经网络就等价于一个概率模型了,比如前面提到的统计语言模型。
关于人工神经网络的训练,一般情况下,在拥有大量训练数据时,我们定义一个cost function,然后按照梯度下降法找到让成本达到最小的参数,当然除了书中提到的外,还有很多值得我们去深入学习的内容,例如,反向传播导致梯度消失和爆炸,以及衍生的用于不同场景的深度学习模型,例如用于图像的CNN、用于推荐的DeepFM等。
上述都是在有大量训练数据时的选择,当我们无法获得大量标注好的数据时,就需要借助无监督的训练得到人工神经网络的参数。此时,我们需要定义一种新的成本函数,它能够在不知道正确的输出值的情况下,确定(或者预估)训练出的模型是好是坏。最简单的,我们希望分完类后,同一类样本应该靠的比较近,而不同类比较远,这样就可以把每一个样本点到训练出来的聚类中心(Centroid)的欧氏距离作为成本函数。对于估计语言模型的条件概率,就可以用熵作为成本函数。定义了成本函数后,就可以用梯度下降法进行无监督的参数训练了。对于结构复杂的人工神经网络,它的训练计算量非常大,而且是个Np-Hard问题(梯度下降可能会陷入局部最优),因此有很多机器学习的专家在寻找各种好的近似方法。
需要指出的是,人工神经网络的规模决定了它能做多大的事情,但是要想要人工神经网络上规模并非易事,因为网络节点之间是连接的,它的复杂度会随着网络规模的扩大呈指数上升。幸运的是,从20世纪90年代到2010年,计算机处理能力的增长和云计算的兴起让人工神经网络的用处大大增加,并且因为并行计算,过去训练人工神经网络的方法就必须改变,以适应云计算的要求。Google大脑就是在这样的前提下诞生的,其创新之处也在于利用了云计算的并行处理技术。
Google大脑采用人工神经网络主要有以下三点原因:首先,人工神经网络理论上可以在多维空间“画出”各种形状的模式分类边界,有很好的通用性。其次,人工神经网络的算法比较稳定且通用,可以一次设计长期并多场景使用。第三,人工神经网络容易并行化,被贝叶斯网络则不然。
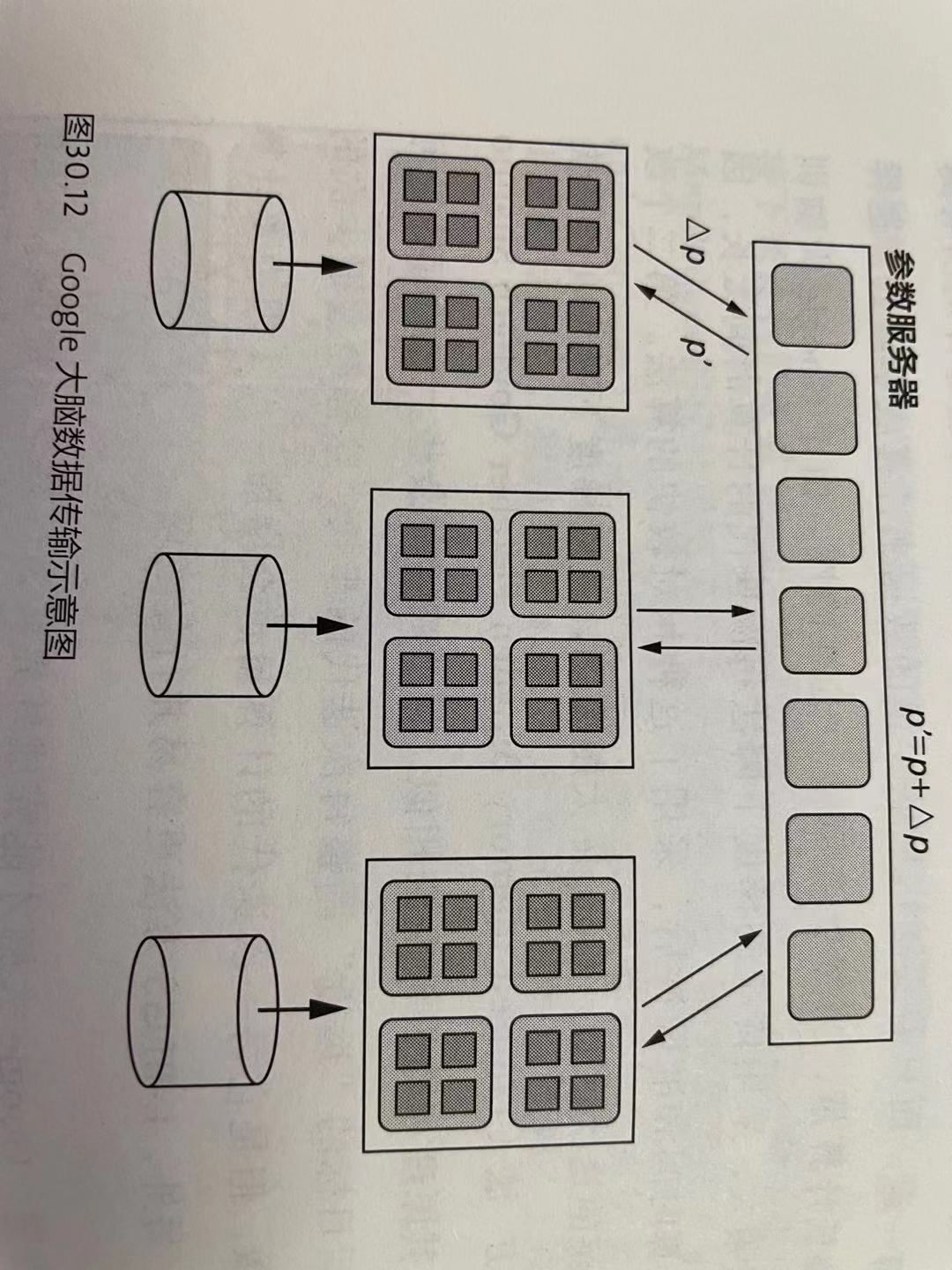
Google大脑的实现与MapReduce的分治思想相似,但是更加复杂。它会把一整个神经网络模型切成数千块,与MapReduce不同,每一块的计算并不是完全独立的,而是要考虑上下左右很多块,相互的关联总数大致和块数的平方成正比,虽然会让这一部分关联的计算变得复杂,但是达到了分解一个大任务成多个小任务的目的。
除了并发训练,Google大脑在减少计算量方面做了两个改进。首先,降低了每次迭代的计算量,Google大脑采用了随机梯度下降(Stochastic Gradient Descent),这种算法秩序随机抽取少量数据来计算成本函数,可以大大降低计算量,虽然会牺牲一点点准确性。第二个改进是减少迭代次数,Google大脑采用比一般梯度下降法收敛的更快的L-BFGS方法(Limited-memory Broyden Fletcher Goldfard Shanno Method),其原理和随机梯度法相似,但是略微复杂一些。它的好处是可以根据离最后目标的“远近”调整每次迭代的步长,这样经过很少次的迭代就能收敛,但是它每一次迭代的计算量也会增加一点(因为要计算二阶导数)。另外,L-BFGS方法更容易并行化计算。借助这两点,Google大脑才能完成外界认为计算量大的难以承受的人工神经网络的训练任务。
㉖人工神经网络与贝叶斯网络
共同点:
1.它们都是有向图,每一个节点的取值只取决于前一级的节点,而与更前面的节点无关,也就是说遵从马尔可夫假设
2.它们的训练方法相似
3.对于很多模式分类问题,这两种方法在效果上相似,也就是说很多用人工神经网络解决的问题,也能用贝叶斯网络解决,反之亦然,但是它们的效率可能会不同。如果把人工神经网络和贝叶斯网络都看成事统计模型,那么这两种模型的准确性也是类似的
4.它们的训练计算量都特别大,大家在使用人工神经网络时要有心理准备
不过,人工神经网络与贝叶斯网络还是有不少差别的:
1.人工神经网络在结构上完全是标准化的,而贝叶斯网络更灵活。Google大脑选用人工神经网络,就是因为看中了它的标准化这一特点
2.虽然神经元函数为非线性函数,但是各个变量智能先进性线性组合,然后对一个变量(即前面组合出来的结果)进行非线性变换,因此用计算机实现起来比较容易。而在贝叶斯网络中,变量可以组合成任意的函数,毫无限制,在获得灵活性的同时,也增加了复杂性
3.贝叶斯网络更容易考虑(上下文)前后的相关性,因此可以解码一个输入的序列,比如将一段语音识别成问题,或者将一个英语句子翻译成中文。而人工神经网络的输出相对孤立,它可以识别一个个字,但是很难处理一个序列,因此它主要的应用常常是估计一个概率模型的参数,比如语音识别中声学模型参数的训练、机器翻译中语言模型参数的训练等,而不是作为解码器
㉗区块链——椭圆曲线加密原理
想要保护私有信息,特别是隐私,必须有一套比对称的机制,做到在特定授权的情况下,不需要拥有信息也能使用信息;在不授予访问信息的权限时,也能验证信息。比特币的意义就在于,它证实了利用区块链能够做到上述这两件事。
㉘量子密钥分发——随机性带来的好处
数据泄露无外乎两种可能:在数据存储的地方被盗取,或者在数据传输的过程中被解惑。要解决这个问题,最好的方法就是对数据进行加密。那么是否存在一种无法破解的密码呢?其实信息论的发明人香农早就指出了,一次性密码从理论上讲永远是安全的。而近年来非常热门的量子通信,便是试图实现加密密钥的安全传输,确保保密通信不被识破。这就是量子密钥分发技术。量子通信并不是像很多媒体曲解的那样——靠量子纠缠实现通信,而是靠光量子的偏振特性承载信息,靠数学和信息论的基本原理保证它的保密性。
光子既是一种粒子,又是一种波,其传播方向与振动方向垂直,这就是爱因斯坦指出的光的波粒二象性。光子的振动频率和偏振的方向都可以人为控制,激光震动的频率已应用到激光通信中,而量子密钥分发利用了光子的偏振特性。即,我们可以在发送方调整光的振动方向来传递信息,比如把光偏振的方向调成水平的,代表0;调成垂直的,代表1。在接收端,我们放置一个垂直的偏振镜就能检测到所传递来的垂直信息,我们收到信号,就认为发送方送来的信息是1。当然,这么做不是很可靠,因为没有收到信号时,不容易确认是对方没有发送,还是发送过来的是0,因此,更好的办法就是在接收方用一个十字交叉的光栅,让垂直和水平的信号都通过,这样就不会把信息0与没有发送信息这件事混淆了。
当然,(激光)光子的偏振方向可以有各种角度,未必一定要是水平或者垂直的,而如果偏振的方向是其他角度,经过一个水平的光栅,它是否能通过就是随机的了。例如,如果发送方发射了一个偏振方向是45°的光子,它经过垂直光栅的概率是50%,即被检测为1的概率为50%、这个信息就是随机的了。
利用这个特性,我们就可以来分发密钥了,具体做法是这样的。首先,发送方和接收方约定好有两组信息编码方式,一组用垂直的偏振光代表1,水平的代表0,另一组则分别用45°和135°代表1和0。其次,发送方采用哪种编码方式完全是随机的,而且是交替进行的,它并不告诉接收方。接收方也随机调整偏振镜(光栅)的方向。此时的期望值如下,有50%的可能接收方和发送方的解调和调制方法一致,另外50%不一致的情况下,又有50%的几率随机蒙对,也就是说,不论接收方如何设置偏振镜解调的方向,最后得到的信息大约有75%是一致的,或者说误码率为25%。
如果在传输过程中,信息被中间的窃听者截获了。由于光子在经过被错误放置的光栅中,光子的偏振方向就无从得知了,得到的是0还是1是完全随机的(可以被认为是噪声)。如果窃听者再将这些信息转发给原本的接收者,接收者得到的信息只有$75% \times 75% = 56.25%$。接下来,如果接收方再将自己的信息发还给发送者确认,发送者就会发现只有56.25%的一致性,这时他们就知道信息被截获了。
解决了信息安全问题后,我们就需要消除信息的不确定性,来确定以下双方通信的密钥。这一步其实非常简单,发送方只要用明码将它调制偏振方向的基传给接收方即可。这样,接收方就知道在哪些信息位它设置对了(其实是蒙对了),然后再用明码把它设置对的信息位告诉发送方即可。此时这个密钥一般有一半传送信息的长度(偏振器设置对的概率为50%),且完全是随机的。上述通信都是明码进行的,但是因为窃听者并不知道原本的信息,所以获知哪些位置应该设置什么样的解调器并没有意义,并没有破坏密钥的安全性。
上述这种通信协议被称为BB84协议,时查理斯·贝内特(Charles Bennett)和吉勒·布拉萨(Gills Brassard)在1984年发表的。后来,人们又在这个协议的基础上进行改进,有了其他的协议,但是其加密和通信原理并没有本质的变化。
在使用上述协议通信的过程中,发送方和接收方需要通过几次通信彼此确认密钥,而这个密钥只使用一次。如果需要继续通信,就需要再产生和确认新的密钥。因此,这种做法实际上是用时间换取通信的安全性。
值得一提的是,量子通信绝不像很多媒体讲的是万能的。加入通信卫星真的被黑客攻击了,或者通信的光纤在半途被破坏了,虽然通信的双方知道有人在偷听,能够中断通信,不丢失保密信息,但是于此同时,它就无法保证正常的信息能送出去了,就如同情报机关虽然抓不到对方的信使,却能把对方围堵在家里,不让消息发出。此外,虽然今天已经实现了上千千米量级的量子密钥分发,但是量子通信从实验到工程,再到商用,还有很长的路要走。
㉙数学的极限——希尔伯特第十问题和机器智能的极限
就如物理学上无法超越的光速极限或绝对零度的极限一样,人工智能的能力有数学的边界。这一边界与技术无关,仅取决于数学本身的限制。具体到今天大家使用的计算机,它有着两条不可逾越的边界,分别是由图灵和希尔伯特划定的。
图灵划定计算机可计算问题的边界:机器智能显得极为强大,靠的是人们找到了让及其拥有智能的方法,即大数据、摩尔定律和数学模型这三个支柱。我们在前面各个章节中所介绍的内容,其实依然只是一部分数学模型而已。这些数学模型将各种形形色色的实际问题变成了计算问题,当然,这里面有一个前提,就是那些问题本质上就是数学问题,而且是可以用计算机计算的数学问题。但是,当计算机科学家们揭开了一个又一个这样的问题的数学本质之后,人们自然会贪心地以为这样的进步是没有极限的,一致浪费时间去解决根本解决不了、可能也没有必要解决的问题。图灵思考问题的方式恰恰和常人一步步进步的方式相反,他会先划定计算这件事情的边界,在他眼中边界内的问题都是可以通过计算来解决的,当然在边界外可能还有更多的问题,它们与计算无关,无法通过计算来解决,因此图灵并不打算考虑它们。图灵就划定了这样一条边界,后人就不必再浪费时间纠结没有意义的事情,也就不必试图超越边界或极限做事情。
计算对应于确定性的机械运动,这保证了在相同条件下计算出来的结果是可重复的,而人的意识则可能来自于测不准原理(量子力学中一个微粒的位置与速度无法同时被准确测量,即越精确的知道速度,就越测不准位置,而人则是由无数的测不准堆积出来的意识)。所以,关于人的意识,图灵认为是不确定的,不属于计算的范畴,如果真是像图灵想的那样,那么宇宙本身就存在着大量数学问题之外的问题。事实上,与图灵同时代的数学家哥德尔在1930年便证明了数学不可能既是完备的,又是一致的,也就是说,一些命题即使是对的,我们也无法用数学证明它们。这被称为哥德尔不完全性定理,它说明数学的方法不是万能的。事实上除了意识上的不确定性,一些数学问题也是无法用数学证明的,今天很多数学问题并没有数学答案,比如不存在一组正整数$x,y,z$,让它们满足$x^3+y^3=z^3$。这个问题实际上是著名的费尔马大定理的一个特例,而这个定理本身已于1994年由英国著名的数学家怀尔斯(Andrew Wiles)证明了,也就是说,它是无解的。当然,不管怎么说,知道一个问题无解也算是有了答案。但是,是否还存在一些问题,我们根本无法判定答案存在与否呢?如果有,那么这类问题显然是无法通过计算来解决的。在这一方面给了图灵启发的是希尔伯特。
1900年,希尔伯特在国际数学大会上提出了23个(当时还无解的)著名的数学问题,其中第十个问题讲的是:
“任何一个(多项式)不定方程,能否通过有限步的运算,判定它是否存在整数解”
所谓不定方程(也被称为丢番图方程,Diophantine equation),就是指有两个或更多未知数的方程,它们的解可能有无穷多个。为了对这个问题有根性认知,我们来看三个特例:
例一 $x^2+y^2=z^2$
这个方程有三个未知数,它有很多正整数解,每一组解其实就是一组勾股数,构成直角三角形的三边。
例二 $x^N+y^N=z^N$
这些方程都没有正整数解,这就是著名的费尔马大定理。
例三 $x^3+5y^3=4z^3$
这个方程是否有正整数解,就不那么直观了。更糟糕的是,我们没有办法一步一步地判定它是否存在整数解。此外,需要指出的是,即使我们能判定它有整数解,也未必找得出来。
希尔伯特第十问题在1970年被苏联数学家尤里·马蒂亚塞维奇(Yuri Matiyasevich)严格地证明了,除了极少数特例,在一般情况下,无法通过有限步的运算,判定一个不定方程是否存在整数解,那么就说明很多数学问题其实上帝也不知道答案是否存在。对于连答案存在都无法判定的问题,答案自然是找不到的,我们也就不用费心去解决这一类问题了。正是希尔伯特对数学问题边界的思考,让图灵明白了计算的极限所在。
第十问题向世人宣告了很多问题我们无从得知是否有解。如果连是否有解都不知道,就更不可能通过计算来解决它们了。更重要的是,这种无法判定是否有解的问题,要远比有答案的问题多得多。即,有答案的问题—>可判定的问题—>数学问题—>所有问题。
那么对于可判定且有答案的数学问题是否都能够用计算机解决吗?那就要看看计算机是怎么设计的了,1963年,图灵提出了一种抽象的计算机的数学模型,这就是后来人们常说的图灵机,图灵机的核心思想就是用机器来模拟人进行数学运算的过程,这个过程其实是在不断重复两个动作:在纸上写或擦掉一些符号,用笔在纸上不断移动书写位置。图灵机这种数学模型在逻辑上非常强大,任何可以通过有限步逻辑和数学运算完成的问题,从理论上讲都可以遵循一个设定的过程,在图灵机上完成。今天的各种计算机也不过是图灵机这种模型的一种具体实现方式。不仅如此,今天那些还没有实现的假想计算机,比如量子计算机,在逻辑上也并没有超出图灵机的范畴,因此,在计算机科学领域,人们就把能够用图灵机计算的问题称为可计算的问题。
是否所有有答案问题都是可计算问题,这一问题依旧有争议,一方面,人们总可以构建出一些类似悖论的数学问题,显然无法用图灵机来解决;另一方面,在现实世界里是否有这样的问题存在,或者说这些构建出来的我呢提是否有意义,很多人觉得暂时没有必要去考虑。但不管怎么讲,依据丘奇和图灵这两位数学家对可计算问题的描述(也就是所谓的丘奇-图灵论题),有明确算法的任何问题都是可计算的,至于没有明确算法的问题,计算也无从谈起。另外,对于理论上可计算的问题,在工程上未必能实现,比如NP-Hard问题,可能需要算到宇宙的尽头,并且图灵机没有存储内容的限制,这在现实中也是不可能的。
联系一下上述的子集关系,即所有问题—>数学问题—>可判定的问题—>有答案的问题—>可计算问题—>工程可解问题—>人工智能问题。这一种层层递进的包含关系,就可以清楚的看到人工智能的边界了。可以看到,理想状态的图灵机可以解决的问题,只是有答案问题的一部分,而在今天和未来,在工程上可以解决的问题都不会超出这个可计算的范畴。
完结撒花✨✨✨
