几乎所有的算法书中，排序算法都是在最开始介绍的算法，不仅仅是因为排序算法非常简单，而且因为排序算法非常基础，在后续其他算法或者处理其他问题时都有广泛的应用。就像我在刷题时，应用到排序就可以直接按时间复杂度$O(nlogn)$计算。所以此次复习算法和数据结构也从排序算法开始，使用到的工具书有<算法4>、<我的第一本算法书>及其app、<labuladong的算法小抄>。刷题网站为leetcode，理论上会把相关主题的题全部刷到，并且整理出笔记与代码沉淀。

一.排序算法

①时间复杂度为$O(n^2)$的排序算法——选择排序、插入排序、希尔排序

选择排序的过程为，首先，找到数组中最小的那个元素，其次，将它和数组的第一个元素交换位置（如果第一个元素就是最小元素那么它就和自己交换）。再次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。这种方法叫做选择排序，因为它在不断地选择剩余元素之中的最小者。

总的来说，选择排序是一种很容易理解和实现的简单排序算法，它有两个很鲜明的特点。其一：运行时间和输入无关。即一个已经有序的数组或是主键全部相等的数组和一个元素随机排列的数组所用的排序时间一样长。一些其他的排序算法可能会更善于利用输入的初始状态。其二：数据移动是最少的。每次在找到最小值时才会进行一次交换，因此选择排序用了N次交换——交换次数和数组的大小是线性关系。我们将研究的其他任何算法都不具备这个特征（大部分的增长数量级都是线性对数或是平方级别）。

插入排序则像整理桥牌一样一张一张的来，将每一张牌插入到其他已经有序的牌中的适当位置，与选择排序一样，当前索引左边的所有元素都是有序的，但它们的最终位置还不确定，为了给更小的元素腾出空间，它们可能会被移动。但是当索引到达数组的右端时，数组排序就完成了。

对于随机排列的长度为$N$且主键不重复的数组，平均情况下插入排序需要$\cfrac{N^2}{4}$次比较以及$\cfrac{N^2}{4}$次交换。最坏情况下需要$\cfrac{N^2}{2}$次比较和$\cfrac{N^2}{2}$次交换，最好情况下需要$N-1$次比较和$0$次交换。其中的情况好坏取决于输入中元素的初始顺序。

我们可以发现在比较好的情况下，即对于部分有序的数组，插入排序可以获得线性的时间复杂度！

PS.衡量一个数组是不是部分有序和有序的程度时，可以用到倒置数量这个指标。倒置指的是数组中的两个顺序颠倒的元素。比如E X A M P L E中有11对倒置：E-A、 X-A、 X-M、 X-P、 X-L、 X-E、 M-L、 M-E、 P-L、 P-E以及L-E。如果数组中倒置的数量小于数组大小的某个倍数，那么我们说这个数组是部分有序的。下面是几种典型的部分有序的数组：❏数组中每个元素距离它的最终位置都不远；❏一个有序的大数组接一个小数组；❏数组中只有几个元素的位置不正确。插入排序对这样的数组很有效，而选择排序则不然。事实上，当倒置的数量很少时，插入排序很可能比本章中的其他任何算法都要快。

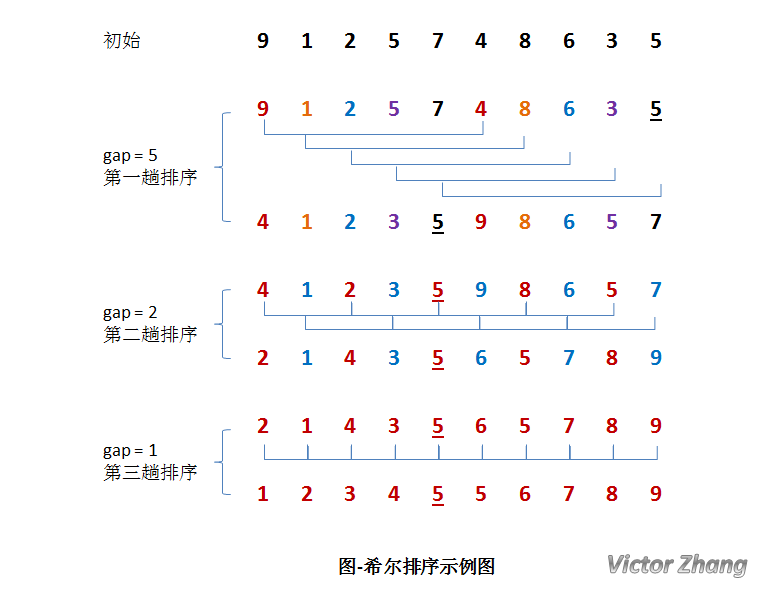
上面我们说到，对于部分有序的数组，插入排序非常有效，那么我们可不可以对数组预处理成部分有序，再用插入排序呢。这就是希尔排序。希尔排序又叫缩小增量排序，它是基于插入排序的增强版。时间复杂度是$O(N*(logN)^2)$，在最坏的请款下比较次数和$N^{\cfrac{3}{2}}$。人们发明了很多递增序列来渐进式地改进最坏情况下所需的比较次数（N4/3,N5/4, N6/5…），但这些结论大多只有学术意义，因为对于实际应用中的N来说它们的递增序列的生成函数（以及与N乘以一个常数因子）之间的区别并不明显。

②时间复杂度为$O(nlogn)$的排序算法——归并排序、快速排序

当我们看到$logn$时不难想到"二分"的思想。

归并排序运行速度比简单排序块，但是它需要的空间是原始数组空间的两倍；通常这是一个严重的缺点。

二.代码沉淀

①有序数组中查找左右边界

def helper(tar): #左边界
    i, j = 0, len(nums) - 1    
    while i <= j:
        m = (i + j) // 2
        if nums[m] < tar: i = m + 1
            else: j = m - 1
     return j

def helper(tar): # 右边界
    i, j = 0, len(nums) - 1
    while i <= j:
        m = (i + j) // 2
        if nums[m] <= tar: i = m + 1
            else: j = m - 1
    return i

②双指针——将两个数组合并

# 有些题中，为了不占用新内存空间，可以使用逆向双指针在原数组上进行
class Solution:
    def merge(self, A: List[int], m: int, B: List[int], n: int) -> None:
        """
        Do not return anything, modify A in-place instead.
        """
        pointera = m-1
        pointerb = n-1
        while pointera >= 0 and pointerb >= 0:
            if A[pointera] >= B[pointerb]:
                A[pointera+pointerb+1] = A[pointera]
                pointera -= 1
            else:
                A[pointera+pointerb+1] = B[pointerb]
                pointerb -= 1

        while pointerb >= 0:
            A[pointerb] = B[pointerb]
            pointerb -= 1
'''题目链接：https://leetcode-cn.com/problems/sorted-merge-lcci/
此题还可以直接把B数组填入A数组中，对A进行排序'''

# 另一些题中，希望两种数字（如奇偶），在特定的位置，可以使用双指针，找到后交换两指针的元素

③python排序实现

------自定义排序
在python中有自定义排序函数,list.sort(key=函数)
sorted_items = sorted(list,key=函数,reverse=False)
可以根据function对一个list进行排序，函数可以返回一个tuple(x[0],-x[1])，表示先根据x[0]排序，如果相同再根据x[1]排序，负号可以达到根据x[1]降序排列的目的
引申的，如果想根据一个元素在list中出现的次数排序，sorted(list,key=lambda x:(list.count(x),-x))，collections.Counter(s)方法可以返回一个字典，表示每个元素的出现次数。对于上述方法的提升---return ''.join([i*j for i, j in sorted([[i, j] for i, j in dict_al.items()], key=lambda x: -x[1])])

------计数排序，当数据种类较少时可以使用
参考例题：https://leetcode-cn.com/problems/relative-sort-array/

④python排列组合实现

------全排列combinations和permutations函数
combinations方法重点在组合，permutations方法重在排列。返回的都是一个iterator。

------回溯递归
def permutation(self, s: str) -> List[str]:
     if len(s) <= 1: #当只剩一个的时候返回
         return [s]
     return list(set(s[i] + perm for i in range(len(s)) for perm in self.permutation(s[:i] + s[i+1:]))) 
    # 此时当每个元素都不同时，不会有相同的返回值，当有基本元素相同时(['a','a','b']三个基本元素就会出现两个"aab")，set()，可以帮助去除重复

def permutation(self, s: str) -> List[str]: # 递归普通写法
    result = []
    def permutation(ans, s):
        if not s:
            return result.append(ans)
        for i in set(s):
            new_ans = i
            new_s = s.copy()
            new_s.remove(i)
            permutation(ans + new_ans, new_s)
    permutation('', list(s))
    return result
-------回溯非递归
class Solution:
    def permutation(self, s: str) -> List[str]:
        n = len(s)
        curr = list(sorted(s))
        end = list(reversed(curr))
        ans = []
        # 生成下一个排列
        while curr != end:
            ans.append(''.join(curr))
            i = n - 2
            # 29631 -> 31269
            while i > 0 and curr[i] >= curr[i+1]:
                i -= 1
            j = n - 1
            while j > i-1 and curr[j] <= curr[i]:
                j -= 1
            curr[i], curr[j] = curr[j], curr[i]
            curr = curr[:i+1] + sorted(curr[i+1:])
        ans.append(''.join(end))
        return ans

⑤python bisect二分查找

"""
bisect 为可排序序列提供二分查找算法
"""
import bisect

#使用bisect函数前需要对列表进行排序，否则虽然可以输出数值，但没有意义
a = [1, 5, 6, 10, 9]
a.sort()
print("最初的列表：", a)

#bisect.bisect 返回某个数在列表中可以插入的位置，但不会插入该数。
#如果这个数与列表中的元素相同，则返回元素后面的位置
print("6在列表中可以插入的位置：", bisect.bisect(a, 6))

#bisect.insort 将某个数插入列表
bisect.insort(a, 7)
print("在列表中插入7：", a)

#处理插入数值与列表元素相同的情况，返回位置，但不会插入该数
#bisect.bisect_left 插入元素左侧位置；bisect.bisect_right 插入元素右侧位置
print("9在列表中可以插入的位置：", bisect.bisect_left(a, 9))
print("9在列表中可以插入的位置：", bisect.bisect_right(a, 9))

#处理插入数值与列表元素相同的情况，插入该数
#bisect.insort_left 插入元素左侧位置；bisect.insort_right 插入元素右侧位置
bisect.insort_left(a, 9)
print("在列表中插入10：", a)
bisect.insort_right(a, 10)
print("在列表中插入10：", a)